40 jaar Uitwiskeling, een terugblik (2)

Vanaf jaargang 11 verscheen Uitwiskeling op een groter formaat. Het pocketformaat werd ingeruild voor een bijna-A4-formaat. In het tweede decennium verscheen op de voorkaft jaarlijks een ander bewijs zonder woorden van de stelling van Pythagoras.

Figuur 1 Een bewijs met zeven puzzelstukken

Typisch voor dit decennium waren de publicaties in verband met de nieuwe technologische mogelijkheden in de wiskundeles. Ze getuigden zowel van vertrouwen in de technologie als van angst voor mogelijk verkeerd gebruik.

In UW 11/4 publiceerde Els Dereymaeker voor het eerst een aantal programma’s voor de TI-82, die ze in haar achturenrichting met de TI-graphlink op het bord projecteerde. Een van deze programma’s berekende het produkt (voor de spellingshervorming van ’96 nog met een k geschreven) van twee complexe getallen. Het was toen nog niet voorgeprogrammeerd in de grafische zakrekenmachine.

Een jaar later, in UW 12/2 schreven we een hele loep over Huiswerk in faxtijd. Faxen was de voorloper van mailen uit de jaren ’80 en ’90. Bij de klassieke huistaak op punten werd er wel eens misbruik vastgesteld door de uitwisseling via de fax tussen klasgenoten. We dachten in deze loep na over alternatieve manieren om huistaken in te zetten in het leerproces.

Ook de vaste computers kwamen op. Niet elke leerling had er eentje maar er was er meestal wel eentje beschikbaar in de klas. Leon Lenders schreef in UW 15/2 een stukje over Stelsels van eerstegraadsvergelijkingen met Derive. Derive was het meest populaire wiskundeprogramma in de jaren ’90. Het was een bijna alwetend programma dat ook bekwaam was in differentiaalvergelijkingen en andere universitaire wiskunde. Commercieel zijn universele programma’s geen goede zet. Daarom is Derive wellicht in de jaren 2000 van de markt gehaald en vervangen door een groot assortiment programma’s met beperktere inzetbaarheid.

De tijd voor de blijde inkomst van de grafische rekenmachine was aangebroken in jaargang 16. Johan, Hilde en Jan schreven een loep over De grafische zakrekenmachine in de tweede graad. Vernieuwend was onder andere de mogelijkheid om te dobbelen met de rekenmachine. Heel even werd ook de symbolische zakrekenmachines aangeraakt, de TI-89, de HP 49G en de Casio CFX 9990. ”Zal de grafische rekenmachine het wiskundeonderwijs veranderen?” was toen de slotvraag, waarvan het antwoord nu bevestigend moet geformuleerd worden. We streefden de voorbije decennia naar een beter evenwicht tussen algebraïsche en numerieke technieken. Er kwam meer nadruk op interpretatie van grafieken, minder op fundering van begrippen.

Kritische stukjes over de digitale hulpmiddelen waren er ook. In UW 17/2 publiceerde Luc Gheysens onder het pseudoniem Luc Janus een bijdrage over ICT-bloopers. Hierin had hij het over ongewenste resultaten door foute instellingen van de zakrekenmachine maar ook over de technische onvolmaaktheden van de zakrekenmachine. Het artikel begon met een fout bewijs dat aantoonde dat \(\pi=3\). Deze bewering werd volmondig beaamd door de zakrekenmachine die uit verstrooidheid was ingesteld op afronden naar een geheel getal.

In het artikel Grafieken met hindernissen uit UW 16/4 werd er wel erg sterk ingezoomd op de excessen van de afrondingen bij het tekenen van gladde functies. Alain Laduraeu (IREM Lille) wees ons op de grafiek van de continue functie \(f:x \mapsto \frac{\ln(e^{x-31}+1)}{e^{x-31}}\) die in het kijkvenster \([0,3]\times[-1,3]\) een grafiek kreeg die gezaagd was als het blad van de haagbeuk, zie Figuur 2. Er werd een verklaring gezocht en gevonden. Door in de gedachtegang van de grafische zakrekenmachine te duiken, werden zelfs de vergelijkingen van de dalende grafieksegmenten achterhaald.

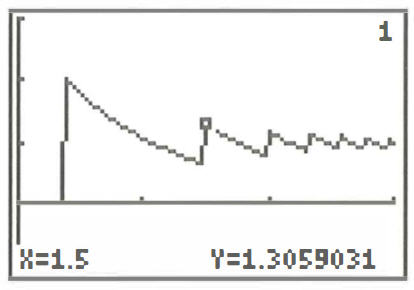
Figuur 2 Een foutje door de afronding in het twaalfde decimaal

Minder alarmerend was het stukje van Dirk De Bock uit UW 12/1 dat we hieronder opnemen. In 1995 al was hij redelijk enthousiast over de mogelijkheid om extremumproblemen numeriek op te lossen. Voor het extremumprobleem van de inhoud van de dubbele kegel hoefden de leerlingen geen (nulwaarden van) afgeleide functies meer te kunnen berekenen. Bij de numerieke benadering van de extrema drongen er zich echter andere vaardigheden op, zie hieronder. Er kwamen meerdere aanvullingen op dit artikel. Ronny Van Meerssche berekende de coördinaten van de toppen van de grafiek met Excel. De vorige maand overleden professor emeritus aan de KU Leuven Edward Omey gaf een theoretische bespiegeling bij het extremumprobleem van de twee kegels.

Begin lesactiviteit

Twee kegels uit één cirkelschijf

Een klassieker onder de extremumvraagstukken is het zgn. kegelprobleem: door uit een cirkelschijf een variabele sector weg te knippen, maakt men een kegel met een vaste schuine hoogte en een variabele inhoud. Het probleem bestaat er dan in om een kegel met een maximale inhoud te bepalen. Het probleem is o.a. befaamd omdat voor het extremum de verhouding van de straal tot de hoogte exact \(\sqrt{2}\) is. Minder bekend maar minstens even verrassend is de volgende variatie op het probleem.

Gegeven is een cirkelschijf waaruit een cirkelsector wordt weggeknipt. Maak van beide sectoren een kegel. Bepaal de sectoren zo dat de som van de volumes van de twee kegels maximaal is.

Eén manier om dit probleem aan te pakken, gaat als volgt. Kies de straal van de cirkelschijf als lengte-eenheid. De lengte van de twee cirkelsectoren is dan \(x\) en \(2\pi-x\).

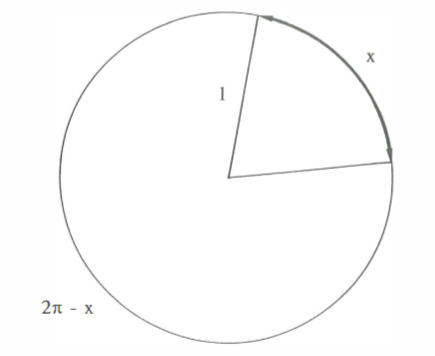
De stralen van de grondvlakken van de kegels zijn dan \(r_1=\frac{x}{2\pi}\) en \(r_2=\frac{2\pi-x}{2\pi}\). De bijbehorende hoogten zijn resp. \(h_1=\sqrt{1-r_1^2}\) en \(h_2=\sqrt{1-r_2^2}\). Grafisch onderzoek van het totale volume \(V=\frac{\pi}{3} \left( r_1^2 \cdot h_1 + r_2^2 \cdot h_2\right)\) in functie van \(x\) (\(0 \le x \le 2\pi\) en \(0 \le V \le 1\)) geeft het volgende beeld met de TI 82.

Deze grafiek en de symmetrie in het probleem doen vermoeden dat er een maximum is voor \(x=\pi\) (twee gelijke kegels!). Eventueel kan men ook analystisch verifiëren dat \(V'(\pi)=0\).

Verder onderzoek toont evenwel aan dat dit vermoeden onjuist is! Door in te zoomen op de grafiek rond het vermoede maximum, krijgen we het volgende verrassende beeld.

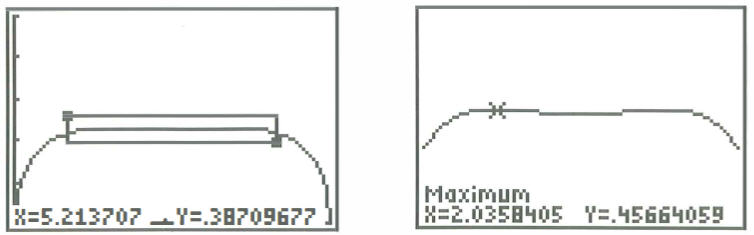
Het nulpunt van \(V’\) bij \(x=\pi\) blijkt dus een (relatief) minimum te zijn. Verder zijn er twee maxima, bij \(x_1 \approx 2,0358405\) en (uiteraard dan ook) bij \(x_2=2\pi-x_1\). Het is mogelijk (maar niet eenvoudig) om, met behulp van een computeralgebrapakket, \(x_1\) exact analytisch te bepalen. Nieuwe interessante informatie brengt dit echter niet aan het licht. De uitdrukking voor \(x_1\) is trouwens behoorlijk ingewikkeld!

Voor mij was het een mooie variatie op een bekend probleem, niet alleen omwille van het onverwachte resultaat, maar ook omdat je de oplossing grafisch kunt bepalen, daar waar analytische methoden extreem lastig zijn.