David M. Bressoud, Princeton University Press, Princeton and Oxford 2019, 221 pp.
Waarom kocht ik dit boek?
Twaalf jaar geleden (Eggermont & Roelens, 2009) schreven wij een uitgebreide loep over de definities in de analyse, waar wij nog steeds helemaal achter staan. We stelden voor om in een eerste fase (die bijna de hele cursus beslaat) consequent te werken met definities die steunen op ‘visuele’ beelden: raaklijn, oppervlakte, ‘gaan naar’, ononderbroken kromme… In wiskundige richtingen zouden we de leerlingen op het einde confronteren met rare functies waarvoor deze visuele beelden niet toereikend zijn. Dat vormt dan de motivatie om iets te zeggen over verfijnde definities, steunend op de \(\varepsilon\)– \(\delta\)-definitie van limiet.
Door deze twee werelden uit elkaar te halen, wilden we duidelijkheid scheppen en geen moeilijke formuleringen aanbieden vooraleer de leerlingen kunnen begrijpen waarom dit nodig is. Eén van onze argumenten was dat historisch, niet toevallig, de afgeleiden en de integralen (Newton, Leibniz, 17de eeuw) een paar eeuwen eerder ontstaan zijn dan hun exacte fundering met het limietbegrip (Cauchy, Weierstrass, 19de eeuw).
Met het bestellen van Calculus reordered wou ik dit graag bevestigd zien. Ik was ook geïnteresseerd om meer te vernemen over hoe de begrippen afgeleiden, integralen, limieten en continuïteit precies ontstaan zijn.
Reordered
Het boek overloopt chronologisch de belangrijke ideeën uit de geschiedenis over integralen, afgeleiden, rijen en reeksen en limieten. Net als wij is de auteur ervan overtuigd dat een eerste cursus over ”calculus’ niet moet starten met de \(\varepsilon\)– \(\delta\)-definitie van limiet, die historisch pas ontstaan is om bepaalde problemen met rare functies op te lossen. Starten met deze verfijnde limietdefinitie is niet alleen problemen oplossen die er op dat moment nog niet zijn, maar is ook beginnen met het moeilijkste begrip. Om integralen en afgeleiden te leren kennen en begrijpen, beperk je je in het begin best tot ‘gewone’ functies en volstaat een intuïtief limietbegrip (‘naderen tot’). Hierover schrijft de auteur in het voorwoord:
The progression we commonly use today [eerst limieten en continuïteit en dan afgeleiden, integralen en reeksen] is appropriate for a course of analysis that seeks to understand all that can go wrong in attempting to use calculus, but it presents a difficult route into understanding calculus.
Een eerste verschil met de loep in Uitwiskeling is dat Bressoud voorstelt om integralen vóór afgeleiden aan te brengen.
Een tweede verschil: Bressoud legt minder de nadruk op de meetkundige betekenissen (afgeleide als helling van de raaklijn, integraal als georiënteerde oppervlakte), die wij in de eerste fase als definities nemen. Hij benadrukt vooral de dynamische processen om integralen en afgeleiden te bepalen. Dit valt meteen af te lezen van de titels van de eerste drie hoofdstukken:
- Accumulation
- Ratios of change
- Sequences of partial sums
- The algebra of inequalities
- Analysis
- Appendix: reflections on the teaching of calculus
Accumulatie is de ‘big idea’ wat een integraal betreft. Bij een afgeleide gaat het essentieel over een verhouding van veranderingen, bij een reeks staat de rij van de partieelsommen centraal. Bij een limiet is de ‘big idea’ het algebraïsche werken met ongelijkheden. Het vijfde hoofdstuk gaat over verdere evoluties in de 19de en de 20ste eeuw en in het laatste hoofdstuk geeft de auteur enkele tips voor het onderwijs.
Bressoud gebruikt overal moderne algebraïsche notaties. Dank zij dit anachronisme is het boek goed leesbaar. Het is een geschiedenis van de grote ideeën, niet van de verpakking ervan… We moeten ons er wel van bewust blijven dat het niet de notaties van toen zijn. Een ander anachronisme gebruikt hij echter niet: hij spreekt niet over wiskundigen maar over filosofen of wetenschappers als het gaat over een tijd waarin de term ‘wiskundige’ nog niet in gebruik was. Pas vanaf ongeveer 1850 werden onze collega’s wiskundigen genoemd…
Het is een interessant boek, het leest vlot en sommige passages zijn heel concreet uitgewerkt en uitgerekend. Mijn eenvoudig idee over de geschiedenis van de analyse, ‘visuele begrippen tot er in de 19de eeuw problemen ontstonden met rare functies en dan pas een verfijnde definitie van limiet’, heb ik met dit boek een beetje moeten bijstellen, zoals je verderop in deze bespreking zult lezen.
We bespreken hieronder zeker niet het hele boek; we beperken ons tot enkele passages. Hier en daar tonen we wat meer details in een kader.
Accumulatie bij Archimedes
Om het volume van een bol te vinden, gebruikt Archimedes een methode met een denkbeeldige balans (zie Roelens & Willems, 2005, p. 29-31 en Roelens, 2018). Het volume van de bol wordt gezien als ‘accumulatie’ van de oppervlakten van vlakke sneetjes die ‘gewogen’ worden met sneetjes van een kegel en van een cilinder. Het is gewaagd: de oppervlakte van de sneetjes worden als massa’s beschouwd in de balans, en er is de dimensiesprong van oppervlakte van sneetjes naar volume van ruimtelichamen. Opvallend is dat Archimedes erg voorzichtig is over de ‘bewijskracht’: hij vindt deze methode wel geschikt om Eratosthenes te overtuigen, naar wie hij deze tekst stuurt, maar niet om te publiceren.
In zijn werk Over de sfeer en de cilinder publiceert hij een ander bewijs, waarin hij het resultaat zorgvuldiger aantoont. Deze zorgvuldige methode van Archimedes komt zelfs heel dicht in de buurt van de verfijnde limietdefinitie van de 19de eeuw. Bressoud illustreert deze methode met een eenvoudiger voorbeeld: de oppervlakte van een cirkel. Het staat in het hoofdstuk over accumulation maar het is ook een voorafspiegeling van algebra with inequalities. Je vindt het bewijs van Archimedes over de oppervlakte van een cirkel in het kader.
De stelling die Archimedes bewijst, luidt:
De oppervlakte van een cirkel is gelijk aan die van een driehoek met als hoogte de straal en als basis de omtrek van de cirkel.
Noem de oppervlakte van de cirkel \(C\) en die van de driehoek \(D\). Archimedes bewijst dat \(C-D=0\) door aan te tonen dat zowel \(C-D>0\) en \(C-D<0\) onmogelijk waar kunnen zijn.
Veronderstel \(C-D>0\). Construeer in de cirkel een ingeschreven veelhoek en noem de oppervlakte van deze veelhoek \(V\). Omdat de veelhoek ingeschreven is in de cirkel, geldt \(C-V>0\). Omdat de veelhoek bestaat uit driehoeken met hoogtes kleiner dan de straal en omdat de omtrek van de veelhoek kleiner is dan die van de cirkel, geldt \(V<D\). Neem nu een ingeschreven veelhoek met dubbel zoveel zijden en noem zijn oppervlakte \(V’\). In figuur 1 zie je dat \(C-V’\) kleiner is dan de helft van \(C-V\). Als je zo verder gaat, kom je een ingeschreven veelhoek tegen waarvan de oppervlakte \(V^*\) voldoet aan \(C-V^*<C-D\).

Figuur 1 C-V’ is kleiner dan de helft van C-V
Dit volgt uit het zogenaamde principe van Archimedes (dat ook al bij Euclides vermeld was):
Als je twee grootheden hebt, de ene groter dan de andere, en je neemt van de grootste steeds meer dan de helft weg, dan zal wat je overhoudt op de duur kleiner zijn dan de kleinste grootheid.
Herken je hierin de ε-n-definitie van \(\lim_{n\to\infty}(\frac{1}{2})^n = 0\)?
We hebben dus \(C-V^*<C-D\) en dus \(V^*>D\). Maar de veelhoek met oppervlakte \(V^*\) is nog steeds ingeschreven in de cirkel en dus \(V^*<D\). Uit deze contradictie volgt dat de veronderstelling \(C-D>0\) niet waar kan zijn.
Analoog, met omgeschreven veelhoeken, toont Archimedes aan dat ook de veronderstelling \(C-D<0\) niet waar kan zijn.
Bijgevolg is \(C=D\); de oppervlakte van de cirkel is gelijk aan die van de driehoek.
Het limietbegrip dat Archimedes hanteert, zonder het zo te noemen, is niet het visuele limietbegrip ‘nadert tot’. Steunend op het visuele limietbegrip zou je simpelweg kunnen zeggen: neem een ingeschreven (of omgeschreven) veelhoek met steeds meer zijden; de oppervlakte van de veelhoek streeft naar die van de cirkel, de omtrek van de veelhoek naar de omtrek van de cirkel en de hoogte van de driehoekjes naar de straal van de cirkel. En klaar zou Kees zijn.
Dit fragment van Archimedes nuanceert onze uitspraak dat het verfijnde limietbegrip van veel latere datum is dan de afgeleiden en de integralen. Dit klopt wel, maar er waren wel al \(\varepsilon\)– \(\delta\)-redeneringen avant la lettre, zoals dit bewijs van Archimedes.
Accumulatie bij ibn Qurra en al-Haytham
Het hoofdstuk over integralen (accumulatie) bevat natuurlijk nog veel andere voorbeelden. Interessant, als mooi voorbeeld van het werken met riemannsommen en inverse functies avant-la-lettre is de (her)ontdekking van het volume van een paraboloïde door Thabit ibn Qurra (9de eeuw) en ibn al-Haytham (11de eeuw).
Thabit ibn Qurra kenmerkt de parabool als bestaande uit punten waarvan de afstand tot de as evenredig is met de vierkantswortel van de afstand langs de as gemeten. In moderne notaties: \(y=a\sqrt{x}\). (zie figuur 2). Hij zoekt het volume van de paraboloïde voor \(0\le x \le b\).
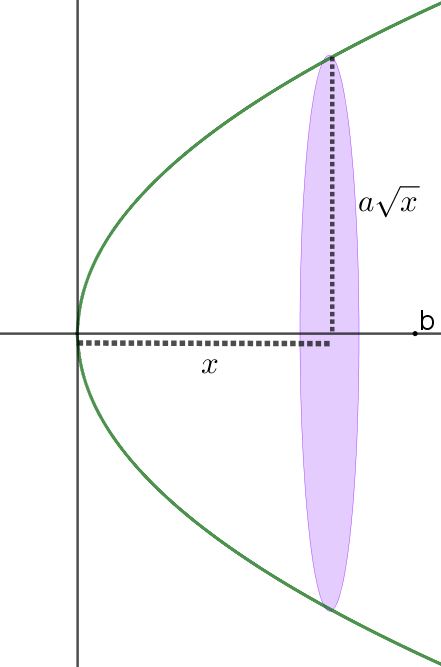
Figuur 2 Wentelende parabool bij ibn Qurra
De oppervlakte van de dwarsdoorsnede bij een willekeurige \(x\) is \(\pi (a\sqrt{x})^2=\pi a^2 x\). Hij snijdt de paraboloïde in plakjes van dikte \(\frac{b}{n}\). Het volume van het \(i\)-de plakje is
\(\pi a^2 i \frac{b}{n} \cdot \frac{b}{n}=\frac{\pi a^2 b^2}{n^2} i.\)
Hierbij benadert hij de plakjes als cilinders. De som van de volumes van al deze plakjes is
\(\begin{align*} \frac{\pi a^2 b^2}{n^2} (0+1+…+(n-1))&= \frac{\pi a^2 b^2}{n^2} \cdot \frac{n^2-n}{2}\\&=\frac{\pi a^2 b^2}{2}-\frac{\pi a^2 b^2}{2n}.\end{align*}\)
Als \(n\) steeds groter wordt, wordt de tweede term zo klein als we willen. Het volume is dus \(\frac{\pi a^2 b^2}{2}\), de helft van het volume van de omgeschreven cilinder.
Twee eeuwen later gaat ibn al-Haytham hierop verder: hij wentelt de parabool rond een as loodrecht op de as van de parabool. Voor de details verwijs ik naar het boek.
Accumulatie in de 17de eeuw
Het 17de-eeuwse West-Europa kon in dit hoofdstuk natuurlijk niet ontbreken. Bonaventura Cavalieri en Pierre de Fermat vinden resultaten die we nu zouden noteren met
\(\int_a^b x^n dx = \left[\frac{x^{n+1}}{n+1} \right]_a^b.\)
Isaac Newton (ook 17de eeuw) tekent een onder- en een bovensom (figuur 3).
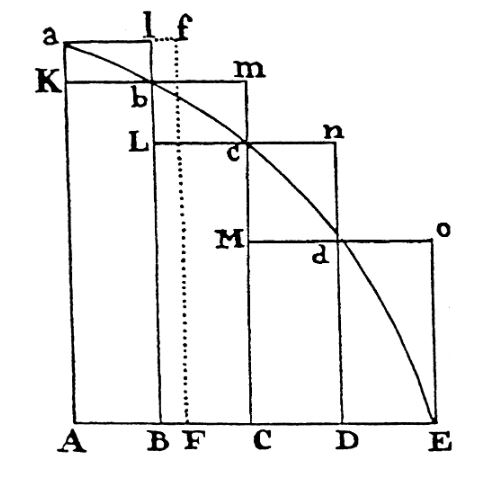
Figuur 3 Figuur van Newton in Philosophiae naturalis principia mathematica, lemma 2
Hij merkt op dat de verschilstukjes tussen beide verschoven kunnen worden boven het lijnstuk \([AB]\). Al die stukjes samen vormen dan de rechthoek \(ABla\). Als \(n\) groter wordt, blijft de hoogte van deze rechthoek gelijk en wordt de basis kleiner. De oppervlakte van deze rechthoek wordt kleiner dan gelijk welke op voorhand gekozen oppervlakte. (Weer een \(\varepsilon\)–\(\delta\)-redenering avant la lettre.)
Accumulatie in de fysica
Het hoofdstuk eindigt met de geschiedenis van een fysische toepassing, het vinden van een afgelegde weg door snelheden te ‘accumuleren’.
Zeno van Elea (5de eeuw v.C.) argumenteert met de paradox van de pijl dat beweging onmogelijk is: hoe zou een pijl kunnen bewegen als hij op elk moment op één bepaalde plaats in de lucht staat? Aristoteles besluit hieruit dat niet de beweging het probleem is, maar dat ‘één moment’ niet bestaat. Hiermee is ook ogenblikkelijke snelheid betekenisloos.
Bij Nicolas van Oresme (14de eeuw) vinden we een figuur die eigenlijk een speciaal geval is van de middelwaardestelling van de integraalrekening (figuur 4).
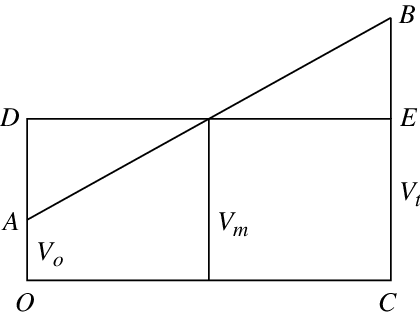
Figuur 4 Figuur van Oresme
Het is merkwaardig dat, toen al, snelheden door (verticale) lijnstukken worden voorgesteld. In het geval van een snelheid die een eerstegraadsfunctie is van de tijd (in fysica: een eenparig versnelde beweging) is de afgelegde afstand gelijk aan de afstand die afgelegd zou worden tegen de gemiddelde snelheid. Eerst gaat het trager, dan sneller en dit compenseert. De oppervlakte van de rechthoek is gelijk aan de oppervlakte onder de kromme. Het straffe is dat Oresme vermeldt dat dit waar blijft als de snelheid ook door een andere kromme gegeven is dan een recht lijnstuk.
Ratios of change
De methode waarbij je een differentiequotiënt \(\frac{f(x+h)-f(x)}{h}\) vereenvoudigt door de teller te ontbinden en \(h\) te schrappen, en waarbij daarna \(h=0\) ingevuld wordt, is afkomstig van Fermat. Volgens René Descartes legde Fermat het niet duidelijk uit: ”[hij verkrijgt het}] à tâtons et par hasard”.
In het kader hieronder zie je hoe Newton over de hoofdstelling van de integraalrekening denkt.
Newton beschouwt een punt \((x,y)\) dat beweegt langs een grafiek. Voor hem is de afgeleide van \(y\) naar \(x\) de verhouding van de snelheid waarmee \(y\) toeneemt tot de snelheid waarmee \(x\) toeneemt, dus eigenlijk (met de Leibniz-notaties die nu nog in gebruik zijn; Newton gebruikte andere notaties):
\(\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\frac{\mathrm{d}y}{\mathrm{d}t}}{\frac{\mathrm{d}x}{\mathrm{d}t}}.\)
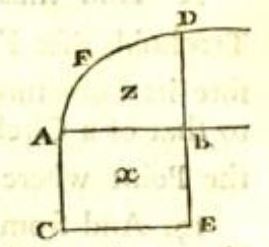
Figuur 5 Figuur van Newton in Method of fluxions and infinite series, problem V
Wij zouden hier \(A\) de oorsprong noemen, \(|AB|\) de abscis \(x\) en \(|BD|\) de ordinaat \(y\). \(D\) beweegt op de grafiek en \(B\) en \(E\), recht daaronder, gaan mee. De hoofdstelling van de integraalrekening (die hij zo niet noemt) zegt
\(\frac{\mathrm{d}z}{\mathrm{d}x}=y=|DB|.\)
Waarom tekent Newton onder \([AB]\) nog een rechthoek? Voor ons lijkt dit overbodig.
Als hij \(\frac{\mathrm{d}z}{\mathrm{d}x}\) zou beschouwen met \(x=|AB|\), dan zou hij een verhouding maken van de snelheid waarmee een oppervlakte verandert en de snelheid waarmee een lengte verandert. Bij verhoudingen moest je altijd gelijksoortige grootheden vergelijken, twee oppervlakten of twee lengtes of twee volumes maar niet een oppervlakte en een lengte! Daarom tekent hij de rechthoek \(ABEC\) met breedte \(|AC|=1\), zodat \(x\) ook een oppervlakte is. Hij bekijkt het verder zo:
\(\frac{\mathrm{d}z}{\mathrm{d}x}=\frac{\frac{\mathrm{d}z}{\mathrm{d}t}}{\frac{\mathrm{d}x}{\mathrm{d}t}}=\frac{|DB|}{|BE|}=\frac{|DB|}{1}=|DB|.\)
(In de tweede gelijkheid gaat hij ervan uit dat de snelheden waarmee \(z\) en \(x\) toenemen wanneer \(D\) op de kromme vooruit gaat, evenredig zijn met \(|DB|\) en \(|BE|\).)
Daarna legt hij uit dat je de vergelijking van de kromme kunt vinden als je een formule hebt voor \(z\) in functie van \(x\). Zijn eerste voorbeeld hierbij is \(z=x^2\):
\(y=\frac{\mathrm{d}z}{\mathrm{d}t}=2x\frac{\mathrm{d}x}{\mathrm{d}t}=2x.\)
want \(\frac{\mathrm{d}x}{\mathrm{d}t}=1\). Verderop doet hij het omgekeerde: de oppervlakte \(z\) bepalen als de vergelijking van de kromme gegeven is.
The algebra of inequalities
Deze paragraaf gaat over de ‘big idea’ wat betreft limieten. Zoals we in de vorige paragrafen gezien hebben, was er al lang vóór de 19de eeuw, naast een intuïtief limietidee en het werken met infinitesimale (oneindig kleine) grootheden, ook een meer rigoureuze behandeling van limieten, zoals bv. bij Archimedes, die in de richting gaat van een \(\varepsilon\)–\(\delta\)-definitie. Het probleem met die rigoureuze aanpak was dat je voor elk geval apart een bewijs moest bedenken. Daarom werkte men in de 17de en de 18de eeuw liever met infinitesimalen, ook al waren deze grootheden, kleiner dan elke positieve grootheid maar toch niet nul, controversieel.
In het eerste boek van de Principia van Newton lezen we een soort definitie van limiet die lijkt op de \(\varepsilon\)–\(\delta\)-definitie:
Quantities, and also ratios of quantities, which in any finite time constantly tend to equality, and which before the end of that time approach so close to one another that their difference is less than any given quantity, become ultimately equal.
Het woord limiet komt er niet in voor, maar wel de tijd, en het lijkt erop dat een functie monotoon stijgend of dalend naar zijn limiet moet gaan (‘constantly tend’)…
Hij ‘bewijst’ ook dat deze grootheden uiteindelijk gelijk worden:
If you deny this, let them be ultimately unequal, and let their ultimate difference be \(D\). Then they cannot approach so close to equality that their difference is less than the given difference \(D\), contrary to the hypothesis.
De omschrijving van het limietbegrip door Augustin Louis Cauchy (19de eeuw) is niet erg verschillend van die van Newton, maar het nieuwe is dat hij concreet rekent met ongelijkheden om bepaalde limieten te bewijzen. Zijn Cours d’analyse start met het bewijzen dat
\(\lim_{x\to 0} \frac{\sin x}{x}=1,\;\;\; \lim_{x\to 0} (1+x)^\frac{1}{x}=e.\)
Nieuw was ook de aandacht voor continuïteit, een begrip dat daarvoor altijd stilzwijgend verondersteld was. Zolang alle functies analytische functies waren (functies die je als machtreeksen kon schrijven), was continuïteit geen issue. Maar het begrip functie werd ruimer, waardoor er functies beschouwd werden waarvan de continuïteit een probleem vormde. Plots kreeg continuïteit een groot belang.
Cauchy definieert continuïteit op basis van limieten: een functie \(f\) is continu in \(x\) als \(\lim_{a\to 0}|f(x+a)-f(x)|=0\). (Cauchy schreef het in een zin en niet met de huidige limietnotatie.) Hij geeft ook een bewijs van de ”tussenwaardenstelling’ voor continue functies, en hij bewijst dat continue functies altijd integreerbaar zijn. Hij maakt wel op een bepaald moment een fout door continuïteit in elke \(x\) van een interval \([a, b]\) te verwarren met gelijkmatige continuïteit in \([a, b]\). In termen van \(\varepsilon\) en \(\delta\) wil dit zeggen dat hij ervan uit ging dat je \(\delta\) enkel moest aanpassen aan de gekozen \(\varepsilon\) en niet aan \(x\).
Analysis
In dit hoofdstuk gaat het over Bernhard Riemann (19de eeuw), die niet enkel een verfijnde definitie van integraal formuleert, maar ook een heel vreemde integreerbare functie construeert, met een soort fractale grafiek en discontinuïteiten in elk interval. Hij voert ook oneigenlijke integralen in. Het vervolg, met Henri Lebesgue, Karl Weierstrass en Georg Cantor bespreken we hier niet meer.
Bronnen
- Eggermont, H., Roelens, M. (2009). Begrippen definiëren in de analyse. Uitwiskeling 25/4, 13-54.
- Roelens, M., Willems, J. (2005). Oppervlakte en volume door de eeuwen heen. Uitwiskeling 21/3, 29-31.
- Roelens, M. (2018). Archimedes en het volume van de bol. Pythagoras 58/2, 22-26. https://pyth.eu/archimedes-en-het-volume-van-de-bol



 Onder de loep
Onder de loep