Stappenplannen kunnen handig zijn. Ze bieden houvast bij het uitvoeren van procedures. Maar er zit ook een andere kant aan: een snelle en handige weg naar het antwoord leidt niet altijd tot het gewenste begrip.
Inleiding
In wiskundeboeken en instructiefilmpjes op internet kun je talloze stappenplannen vinden. In heldere, overzichtelijke stappen worden leerlingen geholpen hun wiskundige problemen op te lossen. Ook in wiskundelessen spelen stappenplannen een rol. Al die stappenplannen ondersteunen het uitvoeren van procedures. De vraag is echter wat leerlingen ervan leren. In dit artikel gaan we in op stappenplannen voor het opstellen van de vergelijking van een rechte en het oplossen van eerstegraadsvergelijkingen.
Stappenplannen voor lineaire verbanden
Binnen het onderwerp lineaire verbanden en eerstegraadsvergelijkingen leren leerlingen allerlei problemen oplossen. Voor een deel gaat het om standaardproblemen die vaak, maar niet altijd, bestaan uit dezelfde stappen. Om leerlingen te helpen deze stappen te onthouden, worden stappenplannen aangeboden. In figuur 1 vind je een voorbeeld voor het opstellen van een formule van een lineair verband.
In vijf stappen wordt, aan de hand van een voorbeeld, beschreven hoe je de formule van een lineair verband vindt als er twee punten gegeven zijn. In het voorbeeld zijn de gegeven punten \((27, 3)\) en \((18, 10)\). Je start met het opschrijven van de algemene formule \(y = ax + b\). In de tweede stap wordt de richtingscoëfficiënt bepaald aan de hand van \(\frac{\Delta y}{\Delta x}\). De derde stap is het invullen van de gevonden richtingscoëfficiënt in de algemene formule. In de vierde stap vul je een punt in om \(b\) te vinden. Als laatste stap schrijf je de vergelijking op. Als leerlingen zelf aan de slag gaan met vergelijkbare opgaven kunnen ze de stappen van het voorbeeld volgen.

Figuur 1: Aantekeningen van een leerling van een door de leraar op het bord aangeboden stappenplan
Ook bij het oplossen van eerstegraadsvergelijkingen zien we stappenplannen. Een voorbeeld vind je in figuur 2.

Figuur 2: Typisch stappenplan voor het oplossen van lineaire vergelijkingen
Stap voor stap wordt beschreven wat de leerling moet doen om de oplossing te vinden. De nadruk ligt op het veegproces: eerst alle haakjes weg, dan alle \(x\)-en naar de linkerkant van het \(=0\)-teken en alle getallen naar de rechterkant.
Deze voorbeelden laten zien hoe een stappenplan een heldere en veilige route naar het antwoord biedt. Door het volgen van alle stappen en precies uit te voeren wat in elke stap beschreven staat, wordt de leerling systematisch van de vraag naar het antwoord begeleid. Iedere stap is overzichtelijk en nauwkeurig omschreven. Het is duidelijk waar de leerling moet beginnen en waar het einde is, namelijk bij de laatste stap. Het opknippen van een complex probleem in overzichtelijke stappen maakt het probleem toegankelijker. Voor het oplossen van standaardproblemen lijkt dit een zeer effectieve methode. Het is echter de vraag of dit de juiste ondersteuning is voor het behalen van doelen die verder reiken dan het kunnen oplossen van deze standaardproblemen.
Wat leren de leerlingen?
Wat leren leerlingen van het uitvoeren van stappenplannen? Op het niveau van de procedure zullen ze er zeker profijt van hebben. De doelen die verder gaan dan de procedure lijken juist moeilijker te behalen. Het gebruik van een stappenplan nodigt immers niet uit om na te denken over de procedure als geheel. Om verder te komen dan het foutloos uitvoeren van de procedure en goed begrip te ontwikkelen, is het nodig dat een leerling overzicht krijgt over deze procedure als geheel en dit als object op zich bestudeert (Sfard, 1991). Het stappenplan in figuur 1 gaat voorbij aan het idee dat die formule op meerdere manieren gevonden kan worden. Hoe stel je de formule op als één van de gegeven punten op de \(y\)-as ligt? In dat geval is de \(b\) meteen duidelijk. Of stel dat één van de punten \(x\)-coördinaat \(1\) heeft. Dan is terugtellen met de richtingscoëfficiënt wellicht handiger om de \(b\) te vinden dan via het invullen van een punt. Stel bijvoorbeeld dat één van de punten \((1,4)\) is en dat de richtingscoëfficiënt \(a\) gelijk is aan \(2\). Het snijpunt met de verticale as is dan \((0,2)\) (via één stap naar links, twee naar beneden). Natuurlijk is deze strategie niet altijd handig, maar soms juist wel. Voor leerlingen is het van belang dat ze de flexibiliteit ontwikkelen om hier op verschillende manieren naar te kunnen kijken. Die flexibiliteit wordt ingeperkt als leerlingen in een toetssituatie gedwongen worden het aangereikte stappenplan te gebruiken.
Beginnen bij stap 2 of verder
De voorgeschreven stappen in een stappenplan kunnen ook in de weg zitten als leerlingen problemen voorgelegd krijgen waarbij het niet nodig is om bij stap 1 van het stappenplan te beginnen, maar bij stap 2 of nog verder. De vraag is in hoeverre leerlingen dan beseffen dat een deel van het oplossingsproces beschreven door het stappenplan al uitgevoerd is. In een beperkte uitbreiding van het onderzoek van Van Stiphout (2011) werd aan een groep van vijftig eerstejaarsstudenten van verschillende studies van de Technische Universiteit Eindhoven gevraagd de vergelijking \((x-5)(x+2)(x-3)=0\) op te lossen.
Ruim de helft van de studenten wist de vergelijking op te lossen: \(x-5=0\) of \(x+2=0\) of \(x-3=0\), dus \(x=5\), \(x=-2\) of \(x=3\). Een deel van de studenten begon met het uitwerken van de haakjes, zie de uitwerking in figuur 3.
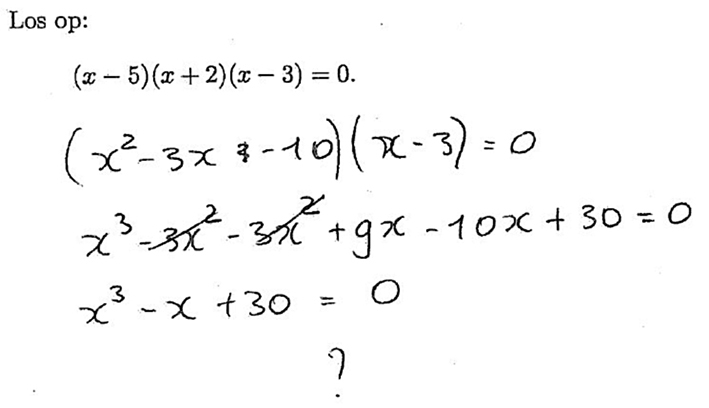
Figuur 3: Uitwerking van een eerstejaarsstudent Technische Universiteit Eindhoven
Deze studenten waren vervolgens niet in staat om te bedenken hoe ze de opgave verder konden oplossen. Ze herkenden niet dat de ontbinding waar ze naar op zoek waren, algegeven was en dat het vinden van de oplossingen erg eenvoudig was. Ze waren niet in staat te ontsnappen aan het automatisme van haakjes wegwerken of, in de woorden van Freudenthal(1983), ‘to unclog an automatism’.
Bij het oplossen van vergelijkingen zien we dat de zekere route naar het einde alleen werkt als het probleem gepresenteerd wordt in de vorm zoals in het stappenplan vermeld. Een kleine afwijking in de vraag die ervoor zorgt dat het stappenplan niet exact meer van toepassing is, heeft mogelijk tot gevolg dat een leerling niet weet wat te doen. Het stappenplan in figuur 2 werkt bijvoorbeeld alleen als de laatste stap van het vegen leidt tot de vergelijking \(x = \text {getal}\). Vergelijkingen van het type waarin de laatste regel leidt tot een tautologie zoals bijvoorbeeld \(x = x\) of een tegenspraak zoals \(x = x – 4\) passen niet in het plan. In het onderzoek van Van Stiphout (2011) werd aan vwo-5-leerlingen de vergelijking \(2(3x + 2) = 3(2x – 1) + 7\) voorgelegd. Uitwerken van de haakjes geeft \(6x + 4 = 6x + 4\), dus iedere \(x \in \mathbb{R}\) is een oplossing. Ruim \(80\%\) van de leerlingen was niet in staat om de juiste conclusie te trekken uit de tautologie die ze vonden. Een robuust begrip van wat ze aan het doen waren of het vermogen om een andere aanpak te kiezen, hadden deze leerlingen niet.
Flexibiliteit
De manier die in een stappenplan wordt beschreven, is niet altijd de kortste of meest elegante manier. Een voorbeeld is de vergelijking
\(\frac {x-1}{2} = 3(x-1).\)
Volgens het stappenplan van figuur 2 werk je eerst de breuk en de haakjes weg wat leidt tot \(x – 1 = 6x – 6\). Vervolgens breng je de \(x\)-en naar links en de getallen naar rechts: \(-5x = 5\). Nog delen door \(-5\) wat \(x = 1\) als oplossing oplevert. Je kan zeggen dat het stappenplan werkt omdat je een oplossing krijgt. We denken echter dat in dit geval een andere manier van kijken interessant kan zijn voor het ontwikkelen van ‘symbol sense’ (Arcavi, 1994). Een onderdeel van symbol sense is het vermogen om globaal naar vergelijkingen te kijken (Gravemeijer, 1990). Dezelfde vergelijking kan dan gezien worden als
\(\frac{1}{2}(x – 1) = 3(x – 1)\)
of als
\(\frac{1}{2}\cdot \triangle = 3 \cdot \triangle.\)
Je kan beredeneren dat zo’n type vergelijking alleen een oplossing heeft als wat onder \(\triangle\) staat gelijk is aan 0 of als \((x – 1) = 0.\)
Het kan ook via de tussenstap
\(\frac{5}{2}(x – 1) = 0.\)

Deze verschillende manieren om deze vergelijking te interpreteren, maken deel uit van de flexibiliteit om met vergelijkingen om te gaan. Die flexibiliteit wordt gezien als een belangrijk onderdeel van symbol sense. Die symbol sense komt mogelijk in de verdrukking bij het rigide gebruik van vaste voorschriften (Alcavi, 1994, Gravemeijer, 1990).
Een ander bezwaar zit in de zorg dat het gebruik van verschillende stappenplannen voor vergelijkbare problemen leidt tot verkokering (Bruin-Muurling, 2010). Hiermee bedoelen we het idee dat voor elk type opgave een aparte strategie wordt aangeleerd. Voor het ontwikkelen van wiskundig inzicht is het juist van belang dat leerlingen de verbinding kunnen maken tussen verschillende typen problemen en de wiskundige concepten die hierachter liggen. Het zoeken naar overeenkomsten en verschillen in verschillende strategieën draagt bij aan het vergroten van het wiskundig inzicht. Ten slotte hebben we bezwaar tegen het beeld dat leerlingen kunnen krijgen van wiskunde. De druk in het onderwijs om leerlingen goede resultaten te laten behalen is hoog (Van Stiphout en Bruin-Muurling, 2016). Dat kan leiden tot een (onbewuste) focus op de vraag hoe leerlingen geleerd kan worden om antwoorden te vinden op (standaard)problemen, ook wel ‘answer getting’ genoemd (Gravemeijer e.a., 2016). Dit is verleidelijk, maar tevens een valkuil omdat het juist met het oog op de toekomst van belang is om te investeren in de onderliggende wiskundige ideeën (Gravemeijer e.a., 2017). Het aanreiken van stappenplannen kan op korte termijn resultaat bieden. Op de langere termijn kan het er echter voor zorgen dat leerlingen wiskunde gaan zien als een vak waarin het gaat om het snel vinden van het antwoord (Askew, e.a., 1997 en Schoenfeld, 1992).
Conclusie en discussie
In dit artikel lieten we zien dat het gebruik van stappenplannen leerlingen houvast kan bieden. Maar er zijn ook nadelen aan stappenplannen. Door nadruk op één enkele manier van oplossen, is er weinig ruimte voor flexibel strategiegebruik die rekening houdt met getal- of gevalspecifieke kenmerken van de opgave. Dit wordt versterkt door het intrainen van stappenplannen waardoor hele sterke automatismen kunnen ontstaan om direct aan een opgave te beginnen, zonder eerst kritisch naar de opgave te kijken. Bovendien dekken de stappenplannen niet altijd alle randgevallen af, of leveren niet altijd de kortste of meest elegante oplossing. Tot slot kan het gebruik van in te trainen stappenplannen verkokering in de hand werken en een beeld van wiskunde als puur instrumenteel bevestigen.
Is het gebruik van stappenplannen dan af te raden? Nee, we willen er zeker niet voor pleiten om stappenplannen niet te gebruiken. Wel denken we dat het van belang is in het gebruik van stappenplannen tegemoet te komen aan bovengenoemde bezwaren. Hiervoor zien we meerdere mogelijkheden. Zo kan leerlingen gevraagd worden om zelf een stappenplan te maken. Op die manier worden leerlingen expliciet uitgedaagd om over het oplossingsproces als geheel na te denken. Een andere mogelijkheid is om bijvoorbeeld in een klassengesprek na te gaan wat voor beperkingen het stappenplan heeft. Hierin kunnen vragen aan de orde komen als in welke gevallen werkt het niet? Of kan het ook anders dan in het stappenplan beschreven? Het kan ook interessant zijn om met leerlingen te onderzoeken voor welk type problemen het stappenplan werkt. Wat als we het probleem iets veranderen? Is het plan dan nog geldig? Op die manier kunnen leerlingen juist worden uitgedaagd om meer flexibel te leren kijken. Uiteraard heeft de leraar hierin een cruciale rol.
Over de auteurs
Irene van Stiphout (irene.vanstiphout@han.nl) is werkzaam als lerarenopleider bij de Hogeschool van Arnhem en Nijmegen en als toetsdeskundige bij het Centraal Instituut voor ToetsOntwikkeling (Nederland).
Geeke Bruin-Muurling (geeke@bruin-muurling.nl) is vakdidacticus en werkzaam als hoofdauteur bij de uitgeverij Zwijsen en als onderwijsvernieuwer.
Bronnen
- Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22(1), 1-36.
- Van Stiphout, I. (2011). The development of algebraic proficiency. PhD thesis, Technische Universiteit Eindhoven, http://alexandria.tue.nl/extra2/719774.pdf.
- Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Dordrecht: Reidel.
- Arcavi, A. (1994). Symbol sense: Informal sensemaking in formal mathematics. For the Learning of Mathematics, 14(3), 24-35.
- Gravemeijer, K. (1990). Globaal kijken, een kenmerk van algebraïsche deskundigheid. Nieuwe Wiskrant, Tijdschrift voor Nederlands Wiskundeonderwijs, 10(2), 29-33.
- Bruin-Muurling, G. (2010). The development of proficiency in the fraction domain: Affordances and constraints in the curriculum. PhD thesis, Technische Universiteit Eindhoven, \newline
http://alexandria.tue.nl/extra2/692951.pdf. - Van Stiphout, I. \& Bruin-Muurling, G. (2016). De verleidingen van het kortste pad. Geraadpleegd op http://www.rekenenwiskunde21.nl.
- Gravemeijer, K., Bruin-Muurling, G., Kraemer, J.- M., \& Van Stiphout, I. (2016). Shortcomings of mathematics education reform in the netherlands, a paradigm case? Mathematical Thinking and Learning, 18(1), 25-44.
- Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., \& Ohtani, M. (2017). What mathematics education may prepare students for the society of future? International Journal of Science and Mathematics Education, 1-19.
- Askew, M., Brown, M., Rhodes, V., Wiliam, D., \& Johnson, D. (1997). Effective Teachers of Numeracy: Report of a study carried out for the Teacher Training Agency. London: King’s College, University of London.
- Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334-370). New York: MacMillan.


