De driehoeksongelijkheid is een heel eenvoudig principe. Er zijn twee redenen waarom ik deze ongelijkheid interessant vind.
- Er is geen specifieke voorkennis voor nodig en toch kun je hiermee oefenen in het ‘bewijzen’. Een beetje zoals bij de grafentheorie.
- Wanneer je andere soorten ‘afstanden’ (metrieken) wilt definiëren (bv. de taximetriek, zie Verhulst 2018), dan is de driehoeksongelijkheid één van de eigenschappen die moeten gelden om van een metriek te kunnen spreken. Vergelijk het met de associativiteit: dit is een eigenschap van bepaalde bewerkingen met getallen, die \(-\;\) samen met andere eigenschappen \(\;-\) als basis kan dienen voor algebraïsche structuren zoals de groepsstructuur.
Voor elk drietal punten \(A\), \(B\), \(C\) in het vlak geldt:
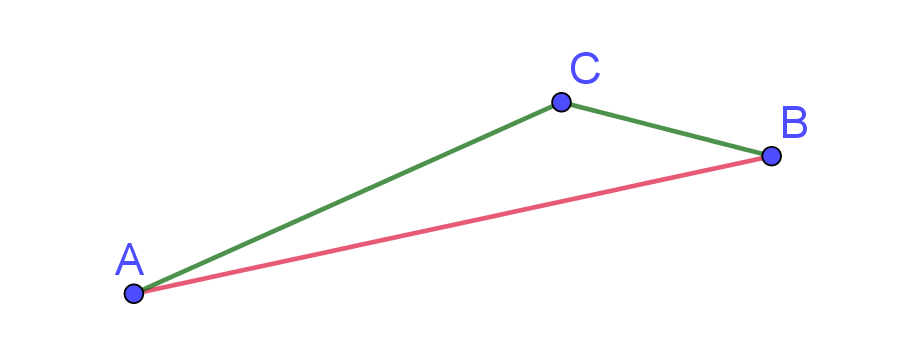
\(|AB|\le|AC|+|CB|\)
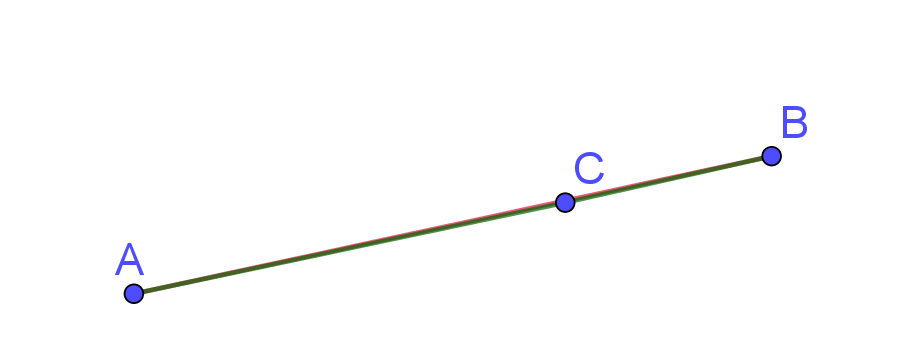
\(|AB|=|AC|+|CB|\Leftrightarrow C\in [AB] \)
In dit artikeltje beperk ik mij tot 1.

‘Recht naar huis hé!’ Als je van punt \(A\) zonder omweg naar punt \(B\) moet gaan, mag je niet via het café \(C\) gaan, want dat is een omweg. Tenzij… het café op je weg ligt. Een meer wiskundige formulering lees je in het kader.
Merk op dat de gelijkheid enkel geldt als \(C\) op het lijnstuk \([AB]\) ligt; op de rechte volstaat niet. Het geval met de gelijkheid wordt de driehoeksgelijkheid genoemd.
Voor hoekpunten van een driehoek geldt steeds de strikte ongelijkheid. In een driehoek is de som van twee zijden altijd strikt groter dan de derde zijde.
Het verschil tussen afstanden en vectoren is dat je bij vectoren altijd de gelijkheid hebt: voor elk drietal punten \(A\), \(B\) en \(C\) geldt \(\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}\). Als je het met vectoren bekijkt, ligt het café altijd onderweg!
Alhoewel Euclides een bewijs gaf voor de driehoeksongelijkheid (Elementen, Boek I, propositie 20), nemen we hier deze regel op intuïtieve (café-)grond aan, zonder bewijs, als spelregel waarop we willen steunen om andere eigenschappen te bewijzen.
In de lesactiviteit hieronder staan enkele bewijsopgaven waarbij je moet steunen op de driehoeksongelijkheid.
Bewijsopgaven
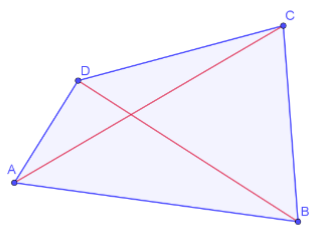
- De som van de diagonalen van een vierhoek is kleiner dan de omtrek. Bewijs dit.
We passen de driehoeksongelijkheid toe in de driehoeken \(ABC\), \(ADC\), \(ABD\) en \(CBD\).
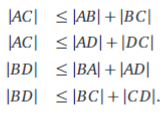
Lid aan lid optellen geeft:
![]() Nu nog beide leden delen door \(2\) en het bewijs is af.
Nu nog beide leden delen door \(2\) en het bewijs is af.
2. Geldt dit ook voor een \(n\)-hoek, met \(n>4\)?
Neen, vanaf \(n=5\) zijn er steeds meer diagonalen en is de som van de diagonalen groter dan de som van de zijden. In de figuur hieronder wordt met ongelijkheden getoond dat dit het geval is voor \(n=5\).
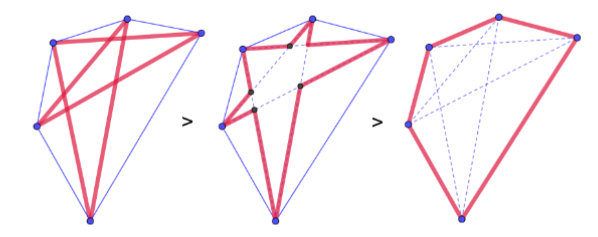
3. Voor welk punt binnen een vierhoek is de som van de afstanden tot de hoekpunten minimaal? Bewijs.
We tonen aan dat dit voor het snijpunt \(E\) van de diagonalen geldt. Immers, voor elk punt \(P\) verschillend van \(E\) binnen de vierhoek geldt:
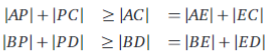
waarbij minstens één van deze ongelijkheden een strikte ongelijkheid is. Immers, \(P\) kan eventueel wel op één van de diagonalen liggen maar niet op allebei. Lid aan lid optellen geeft dan de strikte ongelijkheid:
![]()
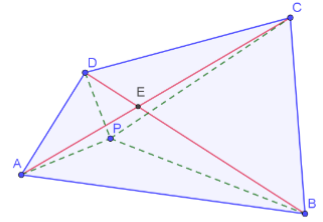
4. Voor een willekeurig punt \(P\) binnen een driehoek \(ABC\) geldt
![]()
Je kunt hier denken aan een elastiekje dat in \(A\) en \(B\) is vastgemaakt. Als je het uitrekt tot punt \(P\), is het minder gespannen dan als je nog verder uitrekt tot punt \(C\). Dit is intuïtief duidelijk, maar als je het wilt bewijzen op grond van de driehoeksongelijkheid, moet je dit ”verder uitrekken’ in twee stappen doen. Verleng \([AP]\) tot punt \(Q\) op zijde \([BC]\) (zie figuur). Dan geldt:
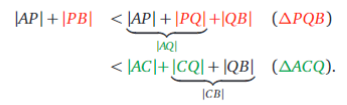
In de berekening hierboven zie je de toepassing van de driehoeksongelijkheid in dezelfde kleur als de arcering van de driehoekjes in de figuur. De accolades zijn toepassing van de driehoeksgelijkheid.
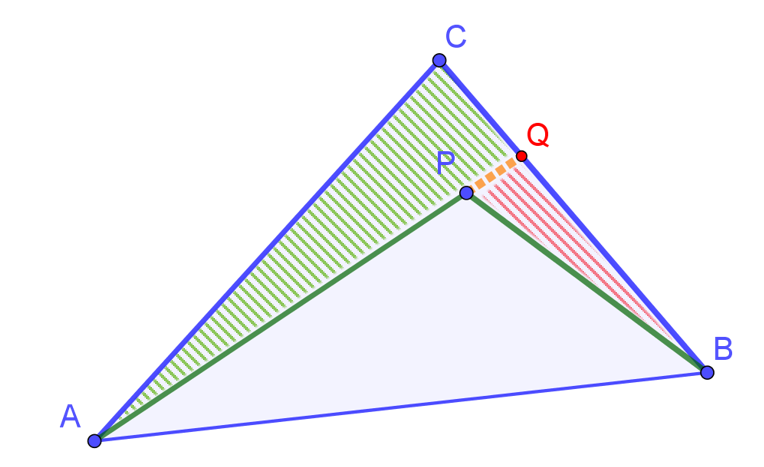
5. Bewijs: voor een willekeurig punt \(P\) binnen een driehoek \(ABC\) met omtrek \(p\) geldt
![]()
Laten we de zijden van de driehoek \(a\), \(b\) en \(c\) noemen en de afstanden van \(P\) tot de hoekpunten \(e\), \(f\) en \(g\) (zie figuur). Eén ongelijkheid verkrijgen we door drie keer de driehoeksongelijkheid toe te passen en lid aan lid op te tellen:
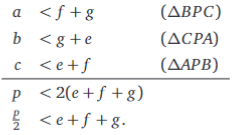
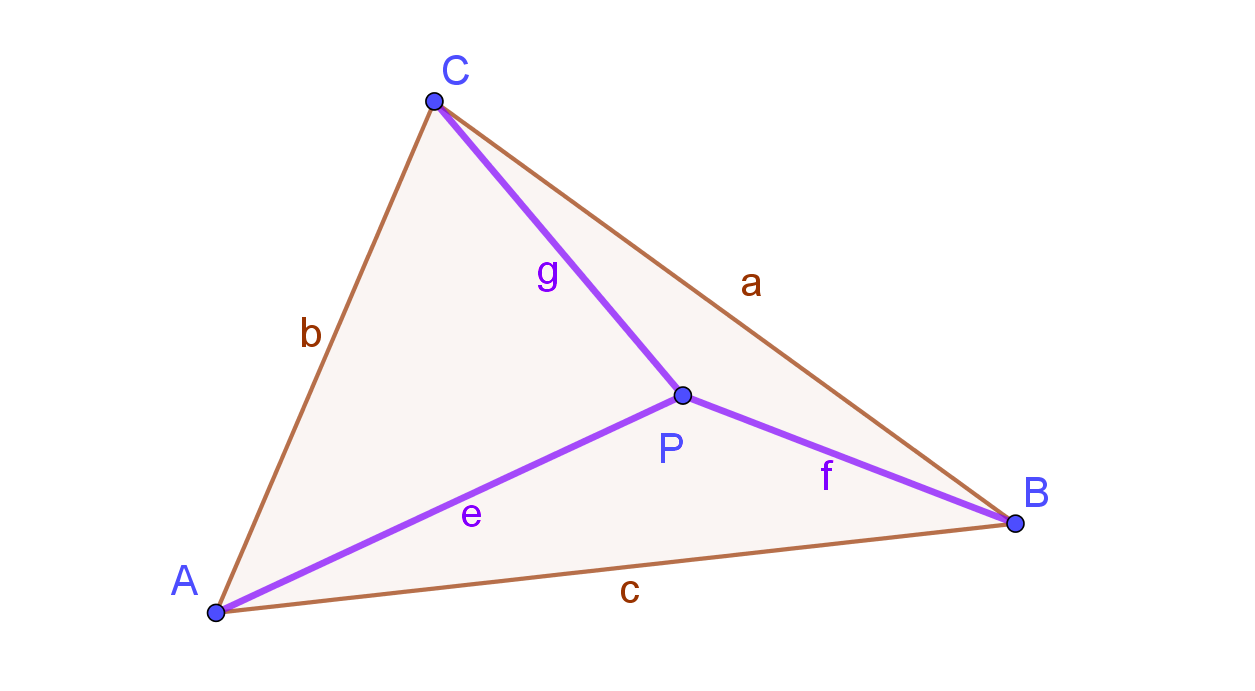
De tweede ongelijkheid biedt wat meer weerstand als we louter met de driehoeksongelijkheid proberen. Maar steunend op wat in vraag 4 bewezen werd, gaat het wel:
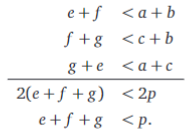
6. Bewijs met de driehoeksongelijkheid dat de afstanden tussen twee punten binnen een cirkel hoogstens gelijk is aan de diameter.
De driehoeksongelijkheid in \(\Delta AMC\) geeft:
![]()
Omdat \(|AM|\) en \(|MB|\) allebei kleiner zijn dan de straal, is \(|AM|+|MB|\) kleiner dan de diameter.
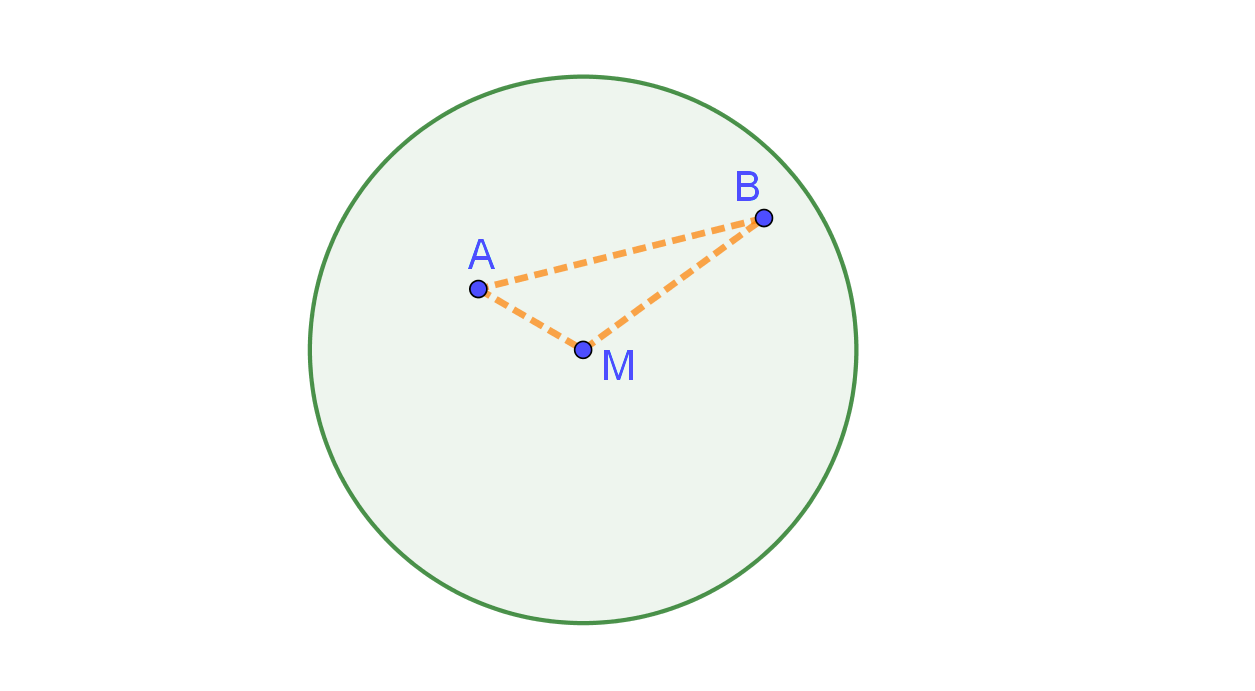 7. Gegeven zijn twee cirkels die elkaar snijden in twee verschillende punten. Wat kun je op basis van de driehoeksongelijkheid zeggen over (1) de afstand tussen de middelpunten en (2) de afstand tussen de snijpunten?
7. Gegeven zijn twee cirkels die elkaar snijden in twee verschillende punten. Wat kun je op basis van de driehoeksongelijkheid zeggen over (1) de afstand tussen de middelpunten en (2) de afstand tussen de snijpunten?
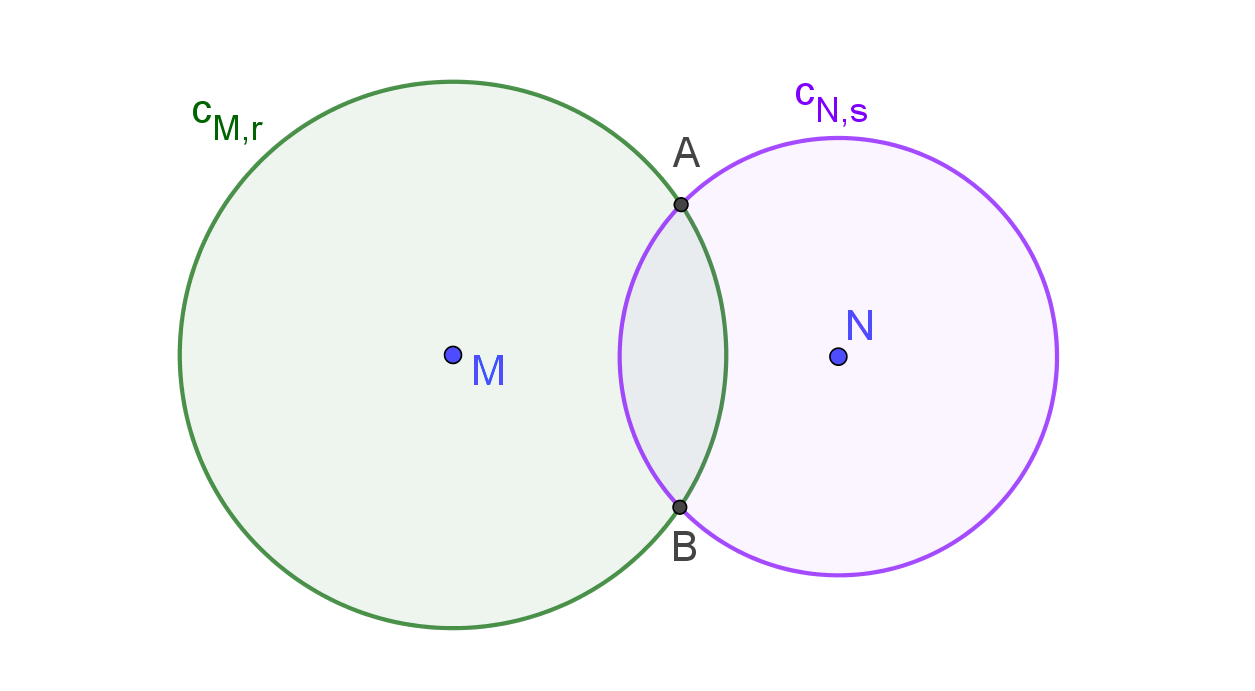
Noem de middelpunten \(M\) en \(N\) en de stralen \(r\) en \(s\). Veronderstel eerst dat \(r>s\). Enerzijds is \(|MN|<|MA|+|AN|=r+s\) (driehoeksongelijkheid in \(\Delta MAN\)). Anderzijds geldt \(|AM|<|MN|+|AN|\) (driehoeksongelijkheid in dezelfde driehoek), dus \(r-s<|MN|\).
Besluit: \(r-s<|MN|<r+s.\)
Laten we nu zoeken naar grenzen voor \(|AB|\). Enerzijds \(0<|AB|\) want in de opgave is er sprake van verschillende snijpunten. Anderzijds is \(|AB|\le|AN|+|NB|=2s\). Merk op dat de gelijkheid hier mogelijk is: het is niet uitgesloten dat \(N\) op één rechte ligt met de snijpunten.
Besluit: \(0<|AB|\le2s\).
Het geval \(s>r\) is natuurlijk analoog. Stel ten slotte dat \(r=s\). Dan verandert er eigenlijk niets behalve dat de laatste ongelijkheid ook strikt is. Immers, \(N\) kan niet op één rechte liggen met de twee snijpunten; dan zouden beide cirkels samenvallen en zitten we niet meer in de situatie met twee snijpunten zoals de opgave het stelt.
Bij vraag 6 is het mogelijk dat leerlingen reageren: ‘dat de afstand tussen twee punten binnen een cirkel kleiner is dan de diameter, dit weten we toch al lang: moet dit bewezen worden?’ Ze hebben zeker een punt, want we situeren ons niet in een formeel systeem waar alle aannames expliciet als axioma’s geformuleerd zijn. De driehoeksongelijkheid hebben we aangenomen zonder bewijs, steunend op intuïtie. En deze eigenschap over twee punten binnen een cirkel is misschien even intuïtief duidelijk als de driehoeksongelijkheid. Dit kan aanleiding zijn tot een discussie over het doel van een bewijs: overtuigen dat de eigenschap waar is (dan is het bewijs hier niet nodig), verklaren waarom de eigenschap geldt (hier hoeft dit ook niet), maar soms ook: de onderlinge afhankelijkheid zichtbaar maken. Hoe is deze eigenschap over de afstand tussen twee punten binnen een cirkel een gevolg van de driehoeksongelijkheid? Hoe past de eigenschap in een systeem waarin de driehoeksongelijkheid één van de spelregels is? Dit is een abstracter doel van bewijzen dan het overtuigen of het verklaren. Maar het kan in de wiskunde zinvol zijn. Als je met een andere metriek werkt dan de euclidische afstand, dan zal een cirkel er anders uitzien dan we gewoon zijn, maar deze eigenschap over twee punten binnen een cirkel zal nog steeds gelden…
Bronnen
- Verhulst (2018). Wiskunde voor bollebozen. Oud-Turnhout: Gompel en Svacina, besproken in Uitwiskeling 35/1.
- Roelens, M. Vlakke figuren. Niet-gepubliceerde cursus.




 Onder de loep
Onder de loep