In de achttiende eeuw had de Russische stad Koningsbergen (vanaf 1946 omgedoopt tot Kaliningrad) gelegen aan de monding van de Pregel, zeven bruggen zoals te zien is op figuur 1. Het klassieke probleem van Koningsbergen verwijst naar deze bruggen. Dit probleem gaat als volgt:
Is het mogelijk om een wandeling door Koningsbergen te maken, precies één keer over elke brug te lopen en op het beginpunt te eindigen?
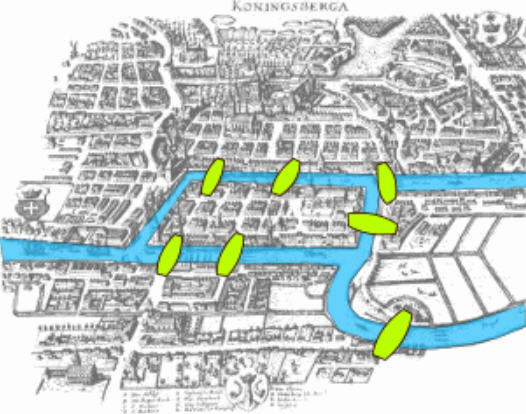
Figuur 1 Bewerkte kaart van Koningsbergen uit Eulers tijd
We kunnen deze kaart wiskundig modelleren door middel van een graaf. Een graaf is een wiskundig object dat bestaat uit knopen (punten) die verbonden zijn met bogen (rechte of kromme lijnstukjes). De bogen stellen hier de bruggen voor en de knopen de vier stukken land die gescheiden worden door de Pregel.
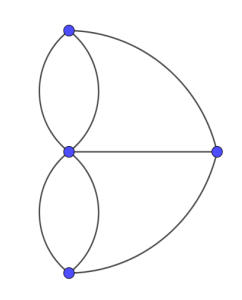
Figuur 2 De graaf van Koningsbergen
Het probleem van Koningsbergen is nu een probleem uit de grafentheorie geworden.
Is het mogelijk om alle bogen in de graaf van Koningsbergen precies één keer te doorlopen in een gesloten wandeling?
De vondst van Euler
Een graaf die op deze manier kan doorlopen worden, noemen we een eulergraaf. Het gesloten circuit dat hiervoor gebruikt wordt, noemen we een eulercircuit. Het probleem vertaalt zich nu als volgt: is de graaf van Koningsbergen een eulergraaf? Met andere woorden: bestaat er een eulercircuit in deze graaf?
De graad van een knoop in een graaf is het aantal bogen die in deze knoop samenkomen. Leonhard Euler (1707-1783) bewees de volgende stelling in 1736:
Als een graaf een eulergraaf is dan zijn de graden van alle knooppunten even.
Wat betekent dit voor de graaf van Koningsbergen? Elk knooppunt in deze graaf heeft een oneven graad (3, 3, 3 en 5). Deze graaf is dus geen Eulergraaf. Er kan geen gesloten wandeling gemaakt worden door elke brug precies één keer over te steken.
Het bewijs van Eulers bewering gaat als volgt. Kies een willekeurig punt \(A\) van de gegeven eulergraaf en noteer met \(n_A\) het aantal keer dat het eulercircuit door het punt A gaat. Omdat een eulercircuit gesloten is, mogen we evengoed aannemen dat \(A\) niet het vertrekpunt is maar een doorgangspunt. Elke keer dat de wandelaar over het eulercircuit in het knooppunt \(A\) toekomt, moet hij ook weer vertrekken. Zo gebruikt hij twee bogen per keer dat hij het knooppunt \(A\) passeert. Het aantal bogen die in \(A\) samenkomen is dus gelijk aan \(2n_A\). Dit aantal is even, wat het bewijs vervolledigt.
De vondst van Hierholzer
We hebben aangetoond dat het enkel bevatten van knopen met een even graad een nodige voorwaarde is voor een graaf om een eulergraaf te zijn. Maar is het ook een voldoende voorwaarde? In 1873 publiceerde Carl Hierholzer (1840-1871) postuum een bewijs dat dit waar is voor samenhangende grafen. Een samenhangende graaf is een graaf waarin men van elke knoop naar elke knoop kan wandelen door bogen van de graaf te volgen. Merk op dat het bewijs van Hierholzer meer dan een eeuw na het bewijs van de stelling van Euler kwam.
Als de graden van alle knooppunten van een graaf even zijn, dan is deze graaf een eulergraaf.
Het bewijs van de stelling van Hierholzer is constructief. Hij bedacht een methode om een eulercircuit te construeren. We beschrijven het algoritme van Hierholzer voor de graaf van figuur 3.
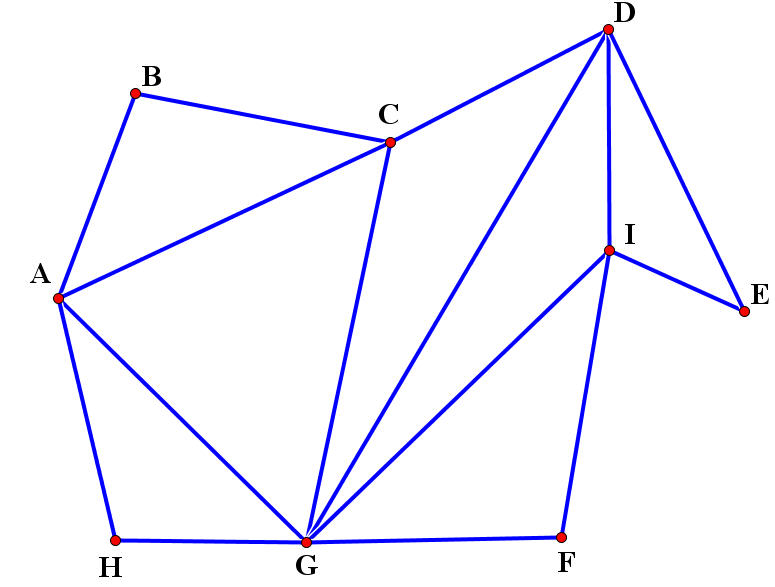
Figuur 3 Het algoritme van Hierholzer
Kies een startpunt, bijvoorbeeld \(A\). Kies een wandeling die start en begint bij dit punt, zo dat geen enkele boog meermaals wordt doorlopen, bijvoorbeeld \(ABCDEIFGHA\). Je kunt uit het ongerijmde bewijzen dat zulk circuit steeds bestaat. Het bewijs van deze deelstelling laten we over aan de lezer. Als tip geven we mee dat je gebruik moet maken van de even graden van de punten in de graaf.
We markeren alle bogen van de graaf die in gebruik zijn genomen door dit eerste circuit. Als er geen ongemarkeerde bogen meer overblijven dan is de eulercircuit gevonden. Als er nog wel ongemarkeerde bogen overblijven, dan kiezen we een nieuw knooppunt van waaruit er ongemarkeerde bogen vertrekken. In dit voorbeeld kan dit het knooppunt \(A\) zijn. Opnieuw zoeken we een circuit over de ongemarkeerde bogen die geen enkele boog meermaals gebruikt. Met dezelfde argumenten kunnen we bewijzen dat dit circuit bestaat. We kiezen bijvoorbeeld \(ACGDIGA\).
Voor de tweede keer markeren we een circuit van de graaf, best met een andere kleur. Op deze manier kunnen we doorgaan totdat alle bogen gemarkeerd zijn. Wat we gedaan hebben, is het verdelen van de graaf in afzonderlijke gesloten circuits, die aan elkaar hangen met minstens één knooppunt. Deze circuits moeten nu nog samengevoegd worden tot één circuit.
Start bij het beginpunt en wandel over het eerste circuit tot je een punt van het tweede circuit tegenkomt. Dan schakel je over op het tweede circuit. Je wandelt over dit tweede circuit tot je een punt van het derde tegenkomt. Zo ga je door tot het laatste circuit. Die kun je helemaal doorlopen. Dan ga je in omgekeerde volgorde verder met de afwerking van het voorlaatste, het derdelaatste, …, het tweede en het eerste circuit. Je eindigt in het beginpunt.
Toegepast op dit voorbeeld, kun je de twee circuits \(ABCDEIFGHA\) en \(ACGDIGA\) in elkaar haken tot \(ABCGDIGACDEIFGHA\).
Toepassingen
Het probleem van de zeven bruggen van Koningsbergen is een voorbeeld van een probleem waarbij grafentheorie kan helpen om een concrete vraag te beantwoorden. Er zijn nog vele andere problemen van die aard, bijvoorbeeld: zoek een geschikte weg voor een vuilniskar die alle straten in een gebied moet bedienen of navigeer volgens de kortste route tussen twee bepaalde plaatsen aangeduid op een wegenkaart. Hierbij werkt men met een graaf waarbij de bogen voorzien zijn van getallen, namelijk de lengten van de straten of de afstanden tussen de steden die met elkaar verbonden zijn.
Merk op dat niet alle stratenplannen eulergrafen zijn. In het geval dat het stratenplan geen eulergraaf is, moeten er denkbeeldige straten bijgemaakt worden tot wanneer alle knooppunten een even graad hebben. Deze bijgevoegde straten ontstaan door sommige wegen twee keer te doorlopen. Het probleem van het circuit van de vuilniskar wordt nu omgevormd tot het vinden van een aantal extra straten met een minimale totale lengte zo dat de graad van alle knooppunten even wordt.
Oefeningen
- Hoeveel bruggen moeten er in Koningsbergen minstens bijgebouwd worden om ervoor te zorgen dat er een gesloten wandeling kan gemaakt worden die elke brug precies één keer benut? Waar liggen deze bruggen dan?
- Is het mogelijk om precies een keer over alle bruggen van Koningsbergen te wandelen zonder terug te keren naar het beginpunt? Zo ja, hoe doe je dit? Een graaf die op deze manier doorlopen kan worden, noemen we een semi-eulergraaf. De bijbehorende wandeling is een eulerspoor.
Oplossingen
- Twee bruggen volstaan. Aangezien de graaf van Koningsbergen vier knooppunten heeft met een oneven graad, is het voldoende om deze knooppunten twee aan twee te verbinden met extra bogen. Zo worden alle graden even. Met één extra boog lukt het niet.
- Stel dat er een eulerspoor bestaat in de graaf van Koningsbergen. Dan kunnen we het begin- en eindpunt van dit pad met een extra boog verbinden tot een eulercircuit. Echter, in de vorige vraag hebben we aangetoond dat één extra boog niet volstaat om van de bestaande graaf een eulergraaf te maken. Het antwoord op deze vraag is dus negatief. We leren hieruit dat een samenhangende graaf een semi-eulergraaf is als en slechts als er precies twee knopen zijn met een oneven graad.
Bronnen
Dit artikel bevat algemeen gekend materiaal uit de grafentheorie. Het is gebaseerd op de cursus Scienteens Lab van de University of Luxembourg, opgesteld door Thierry Meyrath, David Kieffer, Marco Breyer, Gabor Wies, Bruno Teheux en Antonella Perucca.
Figuur 1 is ontleend aan Bogdan Giusca, zie https://upload.wikimedia.org/wikipedia/commons/5/5d/Konigsberg_bridges.png





