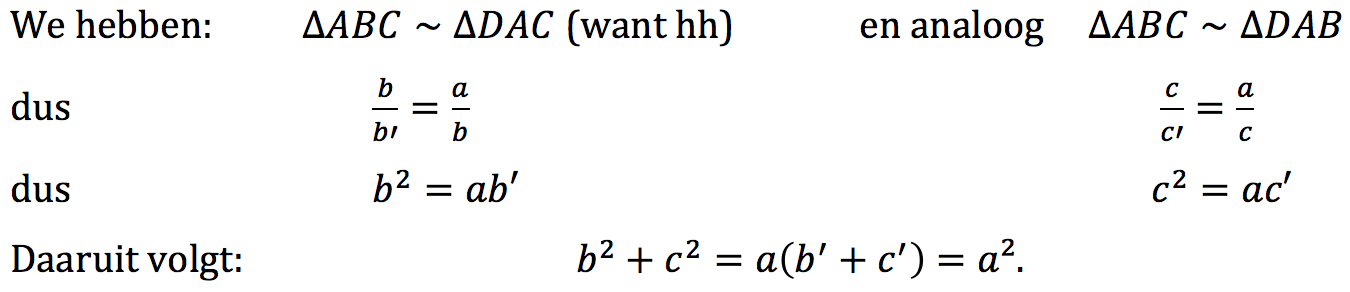6. Problem solving is een zaak van elke dag
Elke les kan als probleemaanpakles gezien worden. Het maakt de lessen boeiender en is ook het wezen van de wiskunde. Wiskunde is immers historisch ontstaan om problemen aan te pakken en de ‘job’ van een wiskundige bestaat in de eerste plaats uit het oplossen van wiskundige problemen.
6.1 Bewijzen
Iets bewijzen is niet het bewijs lezen, dan de stapjes verklaren en tenslotte dit alles van buiten leren voor de punten, maar wel alles willen begrijpen en zoeken naar een verklaring. We willen hier met een voorbeeld laten zien dat je afhankelijk van hoe je een bewijs aanbrengt, meer of minder kansen schept tot ontwikkeling van probleemoplossende vaardigheden. We geven als voorbeeld het bewijs van de stelling van Pythagoras met gelijkvormige driehoeken.
Bewijs van de stelling van Pythagoras met gelijkvormige driehoeken
Gegeven: driehoek \(ABC\) met \(\hat{A}=90°\)
Te bewijzen: \(a^2=b^2+c^2\)
Een klassiek bewijs
Het bewijs bouw je samen met je leerlingen op. Het is de bedoeling dat de leerlingen alle stappen begrijpen.
Teken uit \(A\) de hoogtelijn, \(D\) is het voetpunt.
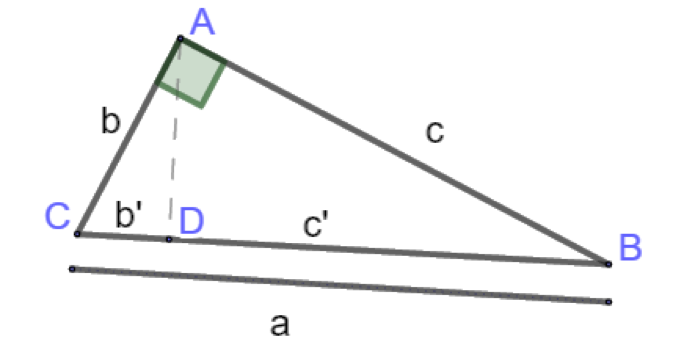
Hetzelfde bewijs als een probleem dat opgelost moet worden
Hoe kom je eraan om de hoogtelijn te tekenen? Dit komt niet uit de lucht gevallen!
We willen \(b^2=\ldots\) en \(c^2=\ldots\) om dan op te tellen.
Leerlingen kunnen op het idee komen om met gelijkvormige driehoeken te werken om een evenredigheid van de vorm \(\frac{b}{\ldots}=\frac{\ldots}{b}\) te verkrijgen, zodat je door de gelijkheid van de kruisproducten \(b^2=\ldots\) uitkomt. Ze hebben dus twee driehoeken nodig met \(b\) als zijde. Hoek \(\hat{C}\) is alvast gemeenschappelijk. Een tweede hoek moet gelijk zijn: \(\hat{A}=90°\). De andere driehoek moet dus ook rechthoekig zijn, en zo kunnen ze zelf op het idee van de hoogtelijn komen.
6.2 Leerstof aanbrengen vanuit een probleem
Je kunt bijvoorboorbeeld het begrip grootste gemeenschappelijke deler aanbrengen met het volgende probleem: een keuken van 3,24 m bij 4,50 m moet gevloerd worden met gelijke vierkante tegels met een zijde die een geheel aantal centimeter is. Je hebt geen tegelsnijder. Je hebt wel de keuze uit een ruim assortiment aan tegelformaten. Wat is de grootste tegel die je kunt gebruiken voor deze keukenvloer?
Leerlingen eerst laten nadenken over een probleem voor je een methode aanleert, werkt het beste. Ze zijn nieuwsgierig naar het resultaat en hun brein is geprikkeld. Het beste moment om nieuwe methodes in te voeren is na het verkennen van een probleem. Leerlingen zijn dan gemotiveerd om een nieuwe methode aan te leren. Bij de aanbreng van de leerstof vanuit een probleem (i.p.v. nadien toepassen op een probleem) moet je nadien wel zorgen voor abstrahering en explicitering los van het probleem.
6.3 Oefeningen
Elke oefening die meer is dan een driloefening, is een probleem, geschikt voor problem solving. Nochtans is drillen noodzakelijk, je moet bepaalde technieken inoefenen om plaats in je brein te krijgen voor andere vaardigheden. Bijvoorbeeld een vergelijking oplossen moet je leren maar na genoeg oefening kun je dit doen zonder dat het nog een probleem is. Voor sommige onderwerpen nemen de oefeningen ook meer de vorm aan van problemen dan voor andere. Zo kun je de afgeleide van een functie (waarvan het voorschrift opgebouwd is uit rationale, irrationale, goniometrische, logaritmische … functies) altijd vinden door de verschillende regels juist toe te passen, maar voor de berekening van een integraal bestaat er niet een enkel algoritme. Je hebt hiervoor een groot arsenaal aan probleemoplossende vaardigheden nodig.
Door aan de opgave van een oefening iets te veranderen kun je meer of minder aan probleemoplossende vaardigheden werken. We geven hieronder een voorbeeld van een oefening in twee versies. Het gaat over de constructie van Heron voor de verdeling van een gegeven lijnstuk volgens de gulden snede.
Constructie van de gulden snede
Deze constructie wordt toegeschreven aan Heron van Alexandrië, eerste eeuw n.C., ook bekend van de formule voor de oppervlakte van een driehoek in functie van de lengten van de drie zijden. Bij de eerste versie van de opgave wordt de constructie gegeven en moeten de leerlingen bewijzen dat ze juist is. De tweede versie is volgens ons interessanter: het zoeken naar de constructie is een probleem dat samen met de leerlingen wordt opgelost. Op die manier zien leerlingen niet enkel in dat de constructie juist is, maar ook hoe men op het idee kan komen om de verdeling volgens de gulden snede op die manier te construeren.
Herhaling: wat is de gulden snede?
Vooraf brengen we in herinnering wat de verdeling volgens de gulden snede is. Gegeven is een lijnstuk . Men wil het lijnstuk in twee stukken verdelen door een punt op te construeren, zodanig dat het langste stuk zich tot het kortste stuk verhoudt zoals het hele lijnstuk tot het langste. Als het langste stuk is, betekent dit dat de volgende evenredigheid moet gelden:
\(\frac{|AQ|}{|QB|}=\frac{|AB|}{|AQ|}.\)

Men kan bewijzen dat deze verhouding van het grote stuk tot het kleine (of van het geheel tot het grote) gelijk is aan het ‘gulden getal’ \(\phi=\frac{1+\sqrt{5}}{2}\). Omgekeerd: als deze verhouding gelijk is aan \(\phi\), dan is het lijnstuk verdeeld volgens de gulden snede.
Eerste versie
Heron verdeelt een gegeven lijnstuk \([AB]\) als volgt volgens de gulden snede. Hij construeert de driehoek \(ABC\) die rechthoekig is in \(B\) en zo dat \(|BC|=\frac{1}{2}|AB|\). Dan construeert hij een cirkel met middelpunt \(C\) door \(B\). Deze cirkel snijdt de schuine zijde \([AC]\) in een punt \(P\). Vervolgens construeert hij een cirkel met middelpunt \(A\) door \(P\). Deze cirkel snijdt \([AB]\) in een punt \(Q\).
Bewijs dat \(Q\) het lijnstuk verdeelt volgens de gulden snede.
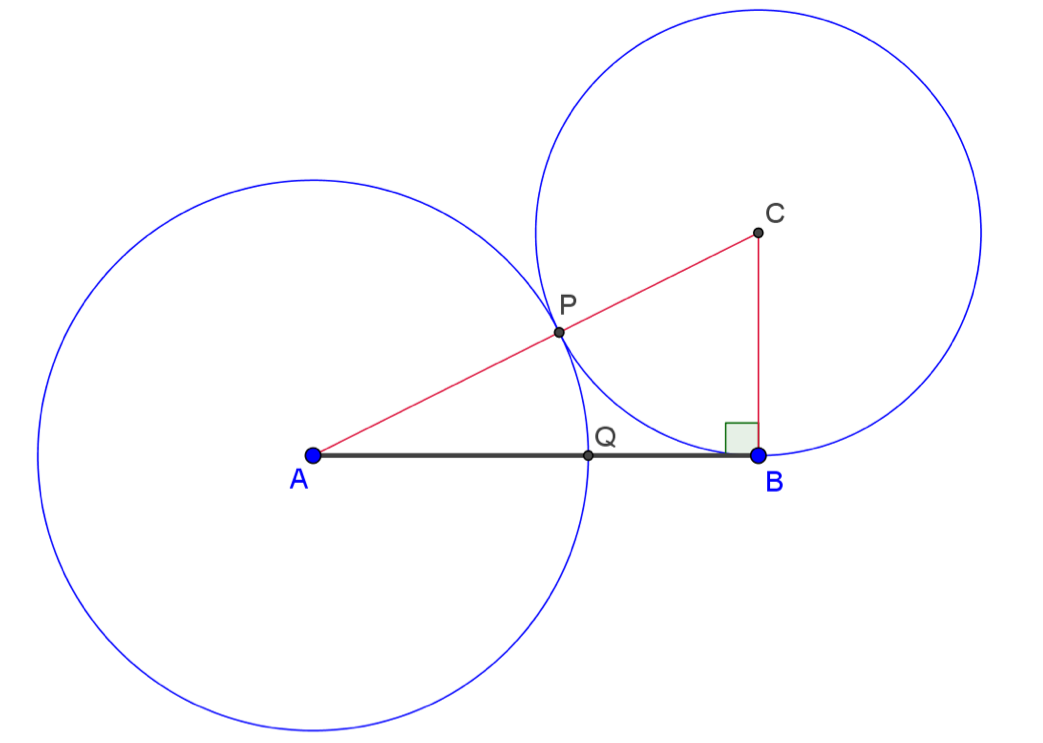
Om dit te bewijzen, kun je
- ofwel bewijzen dat de evenredigheid \(\frac{|AQ|}{|QB|}=\frac{|AB|}{|AQ|}.\) geldt,
- ofwel bewijzen dat \(\frac{|AQ|}{|QB|}=\frac{1+\sqrt{5}}{2}\),
- ofwel bewijzen dat \(\frac{|AB|}{|AQ|}=\frac{1+\sqrt{5}}{2}\).
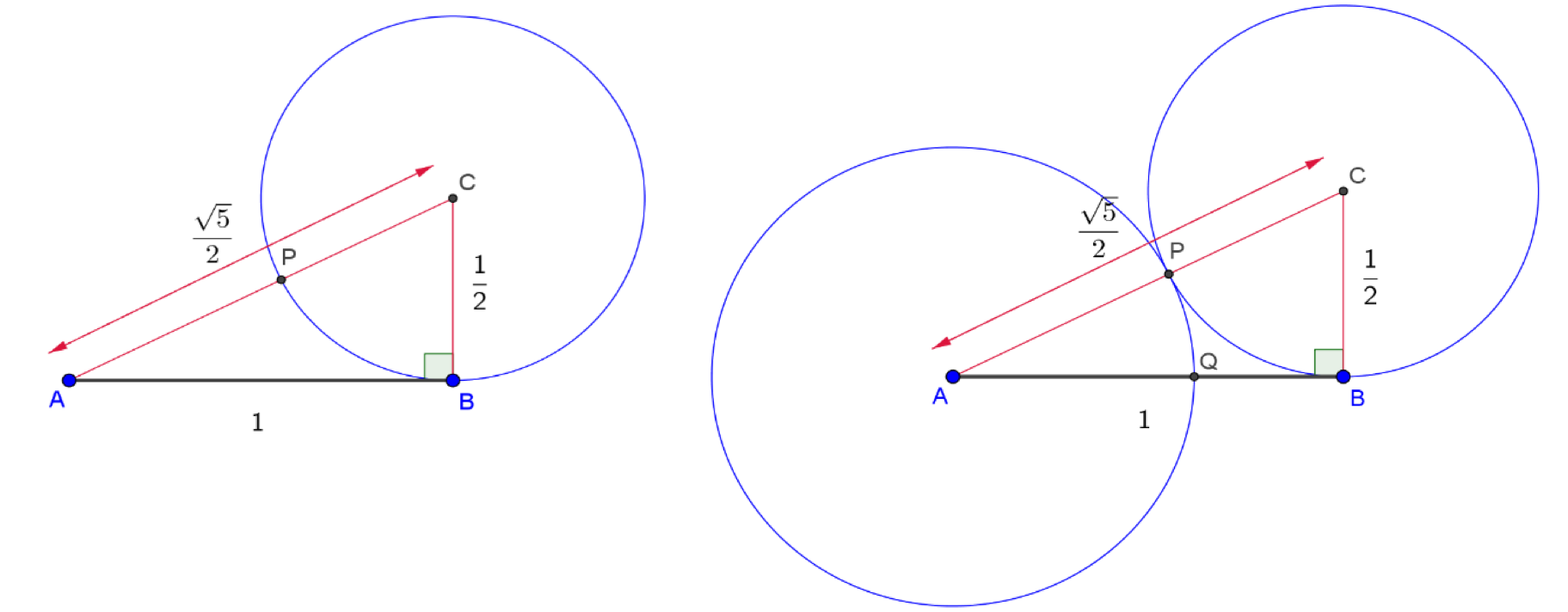
We kiezen voor het laatste. Kies \([AB]\), als lengte-eenheid. Dan is \(|AB|=1\),\(|BC|=|CP|=\frac{1}{2}\) en door de stelling van Pythagoras \(|AC|=\frac{\sqrt{5}}{2}\). Dus:
\(|AQ|=|AP|= \frac{\sqrt{5}}{2}-\frac{1}{2}=\frac{\sqrt{5}-1}{2}.\)
Dit geeft ten slotte:
\(\frac{|AB|}{|AQ|}=\frac{1}{\frac{\sqrt{5}-1}{2}}=\frac{2}{\sqrt{5}-1}=\frac{2\cdot (\sqrt{5}+1)}{5-1}=\frac{1+\sqrt{5}}{2}.\)
Dit bewijs heeft zeker interessante aspecten: de keuze voor één van de drie aanpakvormen, de mogelijkheid om geen letters mee te nemen in de berekeningen door de lengte-eenheid te kiezen, het rekenen met wortels. Maar: de constructie valt eigenlijk uit de lucht.
Tweede versie
Gegeven is een lijnstuk \([AB]\). Hoe kunnen we dit lijnstuk verdelen volgens de gulden snede? Anders gezegd: hoe kunnen we een punt \(Q\) op \([AB]\) construeren zodat \(\frac{|AQ|}{|QB|}=\frac{|AB|}{|AQ|}=\frac{1+\sqrt{5}}{2}\)?
Een constructie vinden doe je niet door meteen naar de passer te grijpen en allerlei cirkelbogen te tekenen. Eerst moet je het probleem analyseren.
We kunnen hier het lijnstuk \([AB]\) als lengte-eenheid nemen en berekenen hoe lang het te construeren lijnstuk \([AQ]\). moet zijn. Dan zien we of we die lengte kunnen construeren.
Welnu:
\(|AQ|=\frac{|AB|}{\frac{1+\sqrt{5}}{2}}=\frac{1}{\frac{1+\sqrt{5}}{2}}=\frac{2}{1+\sqrt{5}}=\frac{2\cdot (1-\sqrt{5})}{1-5}=\frac{\sqrt{5}-1}{2}\).
Als we twee lengtes hebben, kunnen we er het verschil van construeren. Het is dus een goed idee om dit op te splitsen:
\(|AQ|=\frac{\sqrt{5}}{2}-\frac{1}{2}.\)
Lengte \(\frac{1}{2}\) kunnen we zeker construeren want we beschikken over een lijnstuk van lengte 1; een lijnstuk halveren kan met de constructie van de middelloodlijn.
Kunnen we ook een lijnstuk van lengte \(\frac{\sqrt{5}}{2}\) construeren? Wortels worden wel eens met de stelling van Pythagoras geconstrueerd. Gaat dit hier?
\(\frac{\sqrt{5}}{2}=\sqrt{(\ldots)^2+(\ldots)^2}?\)
\(\frac{\sqrt{5}}{2}=\sqrt{\frac{5}{4}}=\sqrt{1+\frac{1}{4}}=\sqrt{1^2+\left(\frac{1}{2}\right)^2}.\)
We moeten dus de schuine zijde construeren van een rechthoekige driehoek met rechthoekszijden 1 en \(\frac{1}{2}\). Van deze schuine zijde moeten we dan de korte rechthoekszijde \(\frac{1}{2}\) aftrekken. Dat kunnen we met een cirkelboog doen. Het lijnstuk \([AP]\) heeft de goede lengte; we moeten het enkel nog op het lijnstuk \([AB]\) overbrengen met een cirkelboog (punt \(Q\)). Hiermee is de constructie gevonden en verantwoord.
6.4. Opgaven die uitnodigen tot discussie
Je kunt met heel eenvoudige probleempjes heel veel bereiken qua probleemoplossend denken. We haalden de mosterd bij Jo Boaler. Ze is een Amerikaanse prof die zich als doel gesteld heeft kinderen en leerlingen beter en liever wiskunde te laten leren. Denken en discussiëren maken sowieso deel uit van wiskundeonderwijs. Ze schreef er ook enkele boeken over die zelfs bestsellers kunnen worden genoemd.
Rijke problemen zijn opgaven die op verschillende manieren kunnen gezien worden, die op verschillende manieren kunnen opgelost en voorgesteld worden. Ze leiden tot nieuwsgierigheid, interesse, verbanden leggen, uitdaging, creativiteit. Door een vraag op een andere manier te stellen of er een ander vraagje aan toe te voegen, kunnen ze veranderen van gesloten, fixedmindsetproblemen naar growthmindsetopgaven met ruimte om veel te leren.
Volgens Boaler kun je niet met het excuus komen dat je hier geen tijd voor hebt in je lessen. Bijna alle oefeningen zijn aan te passen aan deze zienswijze. Hieronder vind je zes vragen die je jezelf kunt stellen om een opgave zo aan te passen dat leerlingen groeien in problemen oplossen. Elke opgave kan beter worden als je aan minstens één van deze zes vragen aandacht schenkt en vaak kun je meerdere vragen combineren.
- Kun je de opgaven verruimen zodat er meerdere oplossingsstrategieën en visuele voorstellingen mogelijk zijn?
- Kun je er een onderzoeksopdracht van maken?
- Kun je het probleem stellen voor je de oplossingsmethode aanreikt?
- Kun je het laagdrempelig en toch uitdagend maken?
- Kun je een visuele component toevoegen?
- Kun je vragen om de redenering uit te leggen of waarom ze een bepaalde methode gebruikten?
We geven enkele voorbeelden waar deze zienswijze gebruikt is.
- Vraag een groep leerlingen in stilte te berekenen. Vraag nadien hoe ze dit berekend hebben en stel het visueel voor (figuur 2).
Door de visuele component toe te voegen, krijg je een andere kijk op deze eenvoudige opgave. Verbluffend op hoeveel manieren dit kan! Dit leidt automatisch tot discussie. Niet iedereen volgt dezelfde strategie, iedereen kijkt anders naar wiskunde. Dit druist in tegen de gangbare visie: wiskunde, het exacte vak met één juiste oplossing! Door op verschillende manieren naar een probleem te kijken, moedig je discussie aan. Belangrijk is ook goed te leren luisteren naar elkaar en respect te hebben voor ieders visie.
- Hoeveel rechthoeken met gehele zijden en met een oppervlakte van 24m² zijn er? Stel ze ook visueel voor.
In plaats van simpelweg een oppervlakte te laten berekenen van een rechthoek van 12 m op 2 m, maak je deze opdracht uitdagender en boeiender.
- Maak met vier 4-en elk natuurlijk getal tussen 1 en 20. Je mag alle bewerkingen gebruiken.
Deze taak kan nog uitgebreid worden: kun je meer dan één methode vinden om elk getal te maken? Kun je ook verder gaan dan 20? Kun je de vier 4-en ook gebruiken om negatieve gehele getallen te maken? Kun je hetzelfde doen met drie 3-en…
- Hoeveel blokjes zal de 100ste figuur in de rij hebben?
- Hoe zie jij het patroon groeien? (Figuur 3)

Figuur 3
Laat eerst de leerlingen individueel zoeken. Door bijkomend te vragen hoe zij het patroon zien groeien, kunnen ze aan elkaar uitleggen hoe zij de groeiwijze zien, hoe ze tellen… Al deze manieren worden visueel ondersteund (figuur 4).
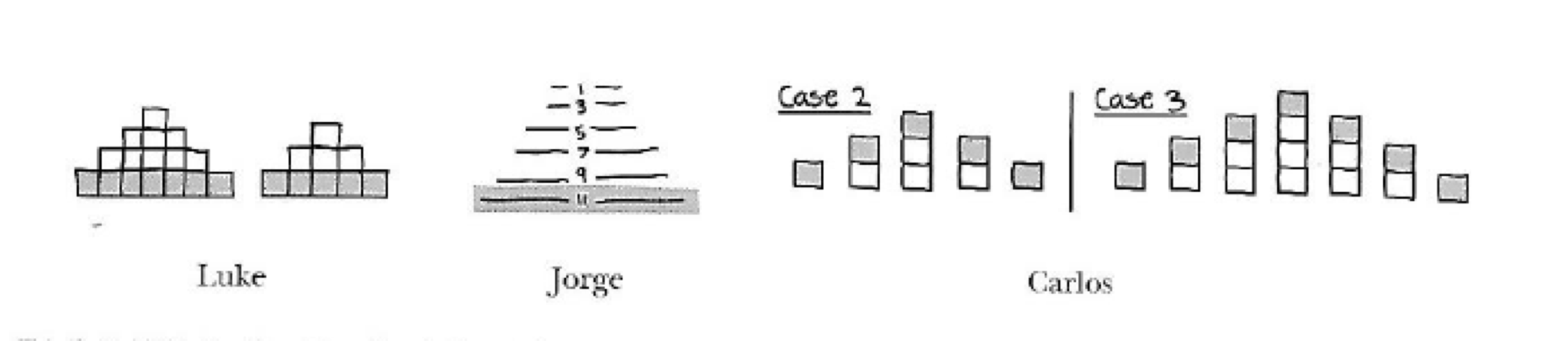
Figuur 4Leerlingen zijn nieuwsgierig naar het resultaat. Visueel denken over groei, geeft inzicht in de manier waarop het patroon groeit. Ze worden aangemoedigd in hun verschillende zienswijzen. Verschillende methodes zijn goed en leiden tot verschillende inzichten over het groeiend patroon. Ze moeten geen schrik hebben om fouten te maken, ze maken gebruik van hun eigen zienswijze en idee, ze werken samen, zelfs in sterk heterogene groepen, de ene abstracter de ander meer visueel. De visuele stap leidt tot veel meer inzicht in het probleem en de oplossing!
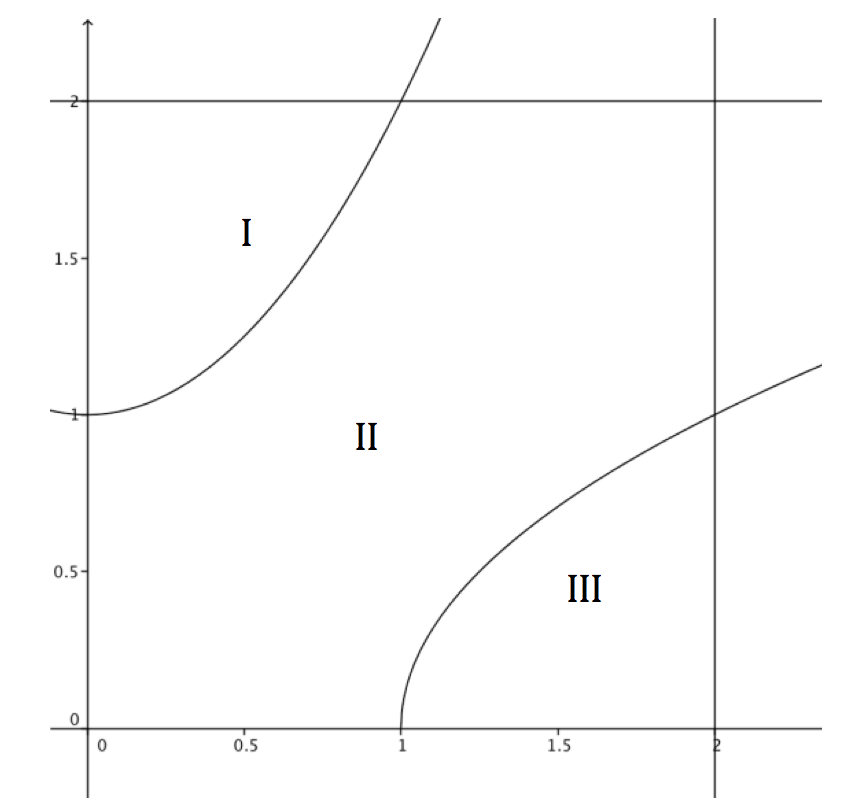
Figuur 5
-
In figuur 5 zie je de grafieken van \(f(x)=x^2+1\) en \(g(x)=\sqrt{x-1}\) en de rechten \(x=2\) en \(y=2\). Met deze formules zijn binnen het vierkant, gevormd door de positieve x-as en y-as en de lijnen \(x=2\) en \(y=2\), drie gebieden te onderscheiden: I , II en III. Bepaal de oppervlakte van elk van de drie gebieden I, II en III op (minstens) twee verschillende manieren. Wees creatief!
Je kon ook gewoon vragen om de oppervlakte III te berekenen. Door te vragen naar minstens twee oplossingsmethodes, zijn de leerlingen verplicht meer uitleg te geven over hun aanpak en het waarom daarvan. Je kunt hen ook enkel vragen naar hun plan van aanpak, eerder dan naar een volledige uitwerking van de oefening. Door dit ook regelmatig op een test op deze manier te vragen, gaan ze dit meer ervaren als iets dat ze moeten leren.
7. Meer lezen…
In deze loep hebben we vooral de rol die je als leraar kan spelen bij het leren oplossen van problemen onderzocht. Er zijn natuurlijk nog veel andere aspecten waar we het niet over hadden. In vroegere artikels kan je daar wat meer over lezen. We geven even een overzichtje:
- jaargang 23 nr. 3: Bibwijzer: Solving mathematical problems,
- jaargang 22 nr. 1: Loep: Problem solving,
- jaargang 8 1: Loep: problemen leren oplossen in de wiskundeles,
- jaargang 3 2: Bibwijzer: On the nature of problems, R. Borasi.
Bronnen
Boaler, J. (2016). Mathematical Mindsets. Unleashing Students’ Potential through Creative Math, Inspiring Messages & Innovative Teaching. San Francisco: Wiley.
Bos, T. (2015). Fasen van zelfsturing: niet gepubliceerde cursus. Hasselt: UCLL.
Gevers, P, Martens, H., Roels, G., Vermesen, R. (1990). Nieuwe Delta 2A Getallenleer. Leuven: Wolters Leuven, 63.
Kumps, L. (s.d.). Het onderzoek van Carol Dweck. In Eduratio. Geraadpleegd 15/2/2018. http://eduratio.be/dweck.html
Op ‘t Einde, P., Hannula, M.S. (2006). The case study of Frank. Educational Studies in Mathematics, 123 – 129.
Pólya, G. (1945). How to Solve It. Princeton University Press. ISBN 0-691-08097-6.
Palha, S, (2013). Shift-problem lessons: fostering mathematical reasoning in regular classrooms. Amsterdam: Universiteit van Amsterdam.
Schoenfeld, A.H. (1985). Mathematical problem solving. Orlando: Academic press.
Zoethout J. (2017). De oplossing ligt in het midden. Pythagoras 56/4, 27-29.



 Onder de loep
Onder de loep